Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 5.12 - Ex. 15
Uma folha de papel contem de matéria impressa, com margem superior de , margem inferior de , margem lateral direita de e margem lateral esquerda de . Determinar quais devem ser as dimensões da folha para que haja o máximo de economia de papel.
Passo 1
Inicialmente, podemos fazer uma ilustração da folha, olha só:
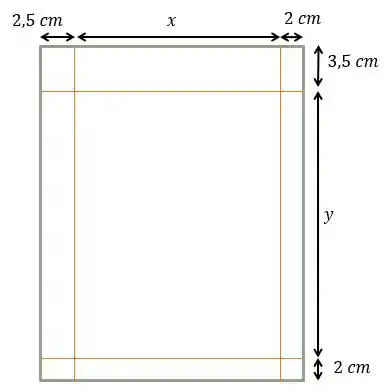
O conteúdo escrito ficará apenas na parte interna da folha. Assim,
E a área total da folha fica o seguinte:
Assim,
Fazendo a distributiva:
Como :
Simplificando:
Passo 2
Para minimizarmos, vamos deixar a equação da área em função apenas de . Depois disso, vamos derivar e igualar a zero para achar os pontos críticos.
Como :
Portanto,
Fazendo as contas:
Derivando,
Igualando a zero:
Assim,
Da equação :
Passo 3
Agora que já sabemos os valores de e , ficou mais fácil encontrarmos as dimensões da folha. A Largura fica assim ó:
Assim,
Já para altura:
logo,