Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 3.3 - Ex. 43b

Neste problema vamos determinar condições sobre p e q de modo que a Eq. (i) possa ser transformada em uma equação com coeficientes constantes através de uma mudança de variável independente. Seja x=u(t) a nova variável independente, com a relação entre x e t a ser especificada mais tarde. Mostre que a Eq(i) torna-se:

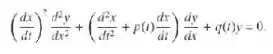
Passo 1

Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para provarmos essa equação. Parece muita coisa, mas é tranquilo. Partiu??

Passo 2

Ok, nosso primeiro passo vai ser relembrar qual a Eq. (i).

y ' ' + p t y ' + q t y = 0

Como o enunciado nos pede para usar a mudança de variável x= u(t), agora é só substituir.

d y d t = d y d x d x d t

Passo 3

Pronto!! Agora é só aplicar a derivada segunda e achar a relação!!

d 2 y d t 2 = d d t d y d t

d 2 y d t 2 = d d t d y d x d x d t

d 2 y d t 2 = d d t d y d x d x d t

d 2 y d t 2 = d x d t d d t d y d x d x d t + d y d x d 2 x d t 2

d 2 y d t 2 = d 2 y d x 2 d x d t 2 + d y d x d 2 x d t 2    

d 2 y d x 2 d x d t 2 + d y d x d 2 x d t 2 + p t d y d x d x d t + q t y = 0    

d 2 y d x 2 d x d t 2 + d 2 x d t 2 + p t d x d t d y d x + q t y = 0

Resposta

d 2 y d x 2 d x d t 2 + d 2 x d t 2 + p t d x d t d y d x + q t y = 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma mola com massa de 3k g é mantida esticada 0.6m além de seu comprimento natural por uma força de 20N . Se a mola começar em sua posição de equilíbrio, mas um empurrão der sua velocidade inicial de
2- Uma mola com uma massa de 4k g tem um comprimento natural de 1m e é mantida esticada até um comprimento de 1.3m por uma força de 24.3N . Se a mola for comprimida até um comprimento de 0.8m e for so
Resolva a equação diferencial ou problema de valor inicial usando o método dos coeficientes indeterminados. y ' ' - 2 y ' + 2 y = x + e x
Resolva a equação diferencial ou problema de valor inicial usando o método dos coeficientes indeterminados. y ' ' - 3 y ' = sen ⁡ 2 x
Resolva a equação diferencial ou problema de valor inicial usando o método dos coeficientes indeterminados. 9 y ' ' + y = e 2 x