Um observador encontra-se na Via Anhanguera em trecho retilíneo, horizontal e situado no mesmo plano horizontal que contém uma torre de TV, localizada no pico do Jaraguá. De duas posições A e B desse trecho retilíneo e distantes 60 m uma da outra, o observador vê a extremidade superior da torre, respectivamente, sob os ângulos de 30° e 31°53'. O aparelho utilizado para medir os ângulos foi colocado 1,50 m acima da pista de concreto que está 721,50 m acima do nível do mar. Determine a altura da torre em relação ao nível do mar.
Dado: tg 31°53' = 0,62.
Passo 1
E aí pessoal, beleza?
Pelo enunciado temos o seguinte desenho:
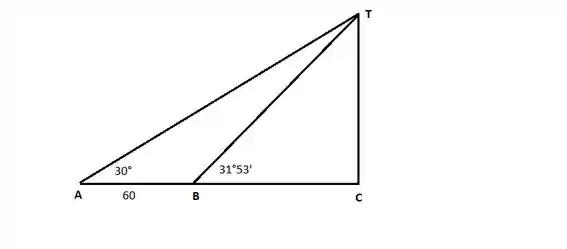
Vamos usar as tangentes para encontrar o valor de CT.
Passo 2
Primeiro a tangente de :
E também a tangente de :
Isolando BC, temos:
Passo 3
Show, agora vamos substituir BC na primeira equação:
Pronto, só falta somar com a distância da pista de concreto ao nível do mar que é 721,5:
Fechou! Vamos pra próxima?