Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 7.3 - Ex. 40

A parábola y = 1 2 x 2 divide o disco x 2 + y 2 ≤ 8 em duas partes. Encontre as áreas de ambas as partes

Passo 1

Fala aí! tudo certinho? 😁

Nesse problema temos um circulo dado por x 2 + y 2 ≤ 8 e uma parábola y = x 2 2 .

Nosso objetivo é obter as areas dentro do circulo acima da parábola e abaixo da parábola.

Tem ideia de como fazemos isso? 🤔

Podemos esboçar um gráfico pra visualizar o que esta acontecendo

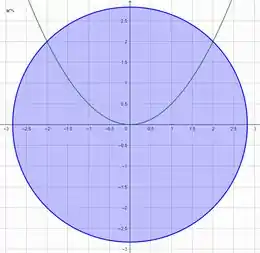
Com isso, podemos ver que os pontos de interseções entre as curvas, são os pontos x = ± 2 , então o que podemos fazer é calcular a area total do círculo e subtrair a área acima da parábola para obter a area dentro do circulo e abaixo da parábola.

Para obter a area acima da parábola podemos calcular a integral ∫ 8 - x 2 - 1 2 x 2 d x onde

x 2 + y 2 = 8 → y = 8 - x 2

y = 1 2 x 2

São as curvas que definem a região.

Veja só! 😊

Passo 2

Agora, basta integrarmos entre x = 2 e x = - 2 ...

A 1 = ∫ - 2 2 8 - x 2 - 1 2 x 2 d x

Podemos fazer uma mudança nesse caso, nos limites de integração devido a simetria das áreas entre - 2 < x < 0 e 0 < x < 2 ...

A 1 = ∫ - 2 2 8 - x 2 - 1 2 x 2 d x = 2 ∫ 0 2 8 - x 2 - 1 2 x 2 d x

Vamos separar em duas integrais...

A 1 = 2 ∫ 0 2 8 - x 2 d x - ∫ 0 2 1 2 x 2 d x

Em ∫ 0 2 8 - x 2 d x , vamos substituir x por 8 sin ⁡ θ e consequentemente d x = 8 cos ⁡ θ d θ .

Dessa forma, convertendo nossos limites de integração, temos

x = 0 → θ = 0

x = 2 → θ = π 4

Aplicando tudo isso na integral...

∫ 0 2 8 - x 2 d x → ∫ 0 π 4 8 - 8 sin ⁡ θ 2 8 cos ⁡ θ d θ

∫ 0 π 4 8 cos 2 ⁡ θ d θ

Pelo teorema fundamental do calculo, sabemos que

∫ cos 2 ⁡ θ d θ = sin ⁡ 2 θ + 2 θ 4

Aplicando os limites de integração

8 ∫ 0 π 4 cos 2 ⁡ θ d θ = 8 sin ⁡ 2 θ + 2 θ 4 0 π 4

8 ∫ 0 π 4 cos 2 ⁡ θ d θ = 2 + π

Tranquilo até aqui? 🤔

Passo 3

Calculando a segunda integral

2 · 1 2 ∫ 0 2 x 2 d x = ∫ 0 2 x 2 d x = 1 6 x 3 0 2

∫ 0 2 x 2 d x = 4 3

Logo

A 1 = 2 + π - 4 3

A 1 = 6 π + 4 3

Para encontrarmos a outra área, basta fazermos

A c = A 1 + A 2

Onde A c é a area do círculo

A 2 = A c - A 1

Se A c = π r 2 , então

A 2 = 8 π - 6 π + 4 3

A 2 = 18 π - 4 3

E aí! entendeu tudo? Responde Aí! 😎

Resposta

A 1 = 6 π + 4 3

A 2 = 18 π - 4 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios de 1 a 38 ache a área limitada pelas curvas dadas. Em cada problema, faça o seguinte: (a) desenhe uma figura mostrando a região e um elemento de área retangular; (b) expresse a área da
Nos Exercícios de 1 a 38 ache a área limitada pelas curvas dadas. Em cada problema, faça o seguinte: (a) desenhe uma figura mostrando a região e um elemento de área retangular; (b) expresse a área da
Nos Exercícios de 1 a 38 ache a área limitada pelas curvas dadas. Em cada problema, faça o seguinte: (a) desenhe uma figura mostrando a região e um elemento de área retangular; (b) expresse a área da
Nos Exercícios de 1 a 38 ache a área limitada pelas curvas dadas. Em cada problema, faça o seguinte: (a) desenhe uma figura mostrando a região e um elemento de área retangular; (b) expresse a área da
Nos Exercícios de 1 a 38 ache a área limitada pelas curvas dadas. Em cada problema, faça o seguinte: (a) desenhe uma figura mostrando a região e um elemento de área retangular; (b) expresse a área da