Uma partícula move-se segunda a lei do movimento , , em que é medido em segundos e em metros
- Encontre a velocidade no instante
- Qual a velocidade depois de
- Quando a partícula está em repouso?
- Quando a partícula está se movendo no sentido positivo?
- Encontre a distância total percorrida durante os 8 primeiros segundos
- Desenhe um diagrama como na figura 2 para ilustrar o movimento da partícula
- Encontre a aceleração no instante e depois de
- Faça os gráficos das funções posição, velocidade e aceleração para
- Quando a partícula está acelerando? Quando está freando?
Passo 1
Opa, temos uma questão com muitos itens! Bora entender o que ela quer da gente!
Temos uma partícula se movendo de acordo com as seguintes expressões:
,
Onde é a posição em metros e é o tempo em segundos.
Na letra (a) queremos a velocidade no instante . A velocidade é a derivada da posição em relação ao tempo, então:
Próxima!
Passo 2
Agora queremos a velocidade depois de . Pra isso pegamos a expressão acima e substituímos :
Esse sinal negativo significa que a partícula esta se movendo da direita para a esquerda!
Passo 3
Ne letra (c) devemos determinar quando a partícula está em repouso. Isso acontece quando:
Logo:
Usando Báskara, ficamos com:
Próxima!
Passo 4
Agora queremos saber quando a partícula está se movendo no sentido positivo. Pra isso devemos ter :
A nossa função é uma parábola com concavidade pra cima, isso significa que, se tem valores positivos e negativos de ela deve começar positiva, ficar negativa e depois positiva de novo.
Como temos os valores das raízes podemos esboçar rapidamente o gráfico:
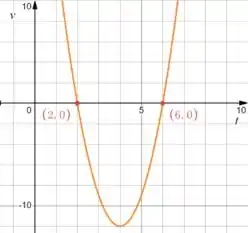
Então a partícula esta se movendo no sentido positivo quando:
Passo 5
Agora queremos a distância total percorrida durante os 8 primeiros segundos, sabemos que a partícula se move no sentido positivo nos intervalos:
Logo, no intervalo de a partícula se move no sentido negativo, então calcularemos a distância para cada intervalo:
Então da distância total :
Passo 6
Agora a gente tem que fazer um diagrama para ilustrar o movimento da partícula. Sabemos pela letra anterior que a partícula anda pra direita nos primeiros segundos. Depois anda pra esquerda nos próximos segundos e finalmente nos últimos segundos ela anda metros pra direita.
Colocando isso em um esqueminha:
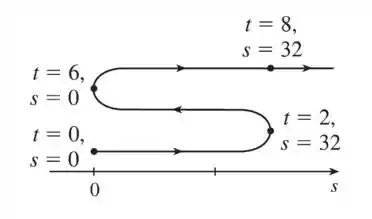
- Esboçando o gráfico
Passo 7
Na letra (g) devemos calcular a aceleração no instante e depois de . A aceletração é a derivada da velocidade em função do tempo, então:
Agora substituindo:
Passo 8
Agora vamos fazeros gráficos das funções posição, velocidade e aceleração para . Temos que:
Fazendo os gráficos, onde :
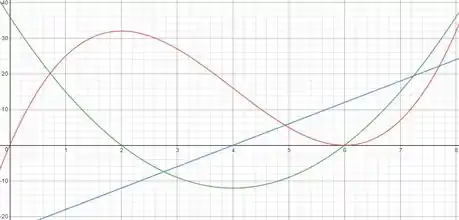
Passo 9
ENFIM O ÚLTIMO ÍTEEEM!!! quando a partícula está acelerando? Quando está freando?
A partícula está acelerando quando e possuem o mesmo sinal. Logo, ela está acelerando no intervalo:
A partícula está freando quando e possuem sinais opostos. Logo, ela está freando nos intervalos:
Poderiamos também ter observado o gráfico do passo anterior!
Prontinho =D
Resposta
Desenvolvimento acima