Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 4.6 - Ex. 20
Use um computador para traçar o gráfico de e para achar Use estes gráficos para estimar os intervalos crescentes e decrescentes, valores extremos, intervalos de concavidade e pontos de inflexão de
Passo 1
Fala aí, pessoal.
Bom, nessa questão teremos que usar um computador pra traçar o gráfico da função . Sendo:
E também para encontra as derivadas e .
A ideia é usar esses gráficos para estimar os intervalos de crescimento e decrescimento, valores extremos, intervalos de concavidade e pontos de inflexão de .
Então vamos lembrar o que cada derivada conta pra gente.
A derivada de uma função é entendida como a inclinação da reta tangente a curva do gráfico da função.
Sabendo disso, podemos pensar que quanto mais positiva a derivada estiver, mais rapidamente a função original estará crescendo.
Assim:
Já a derivada de segunda ordem é a inclinação da reta tangente ao gráfico da primeira derivada e ela nos trará informações sobre o sentido da concavidade.
Assim:
O ponto de inflexão acontece onde a derivada de segunda ordem for igual a zero. Assim:
Agora que já sabemos de tudo isso, bora resolver essa questão.
Passo 2
Vamos começar usando o computador para plotar o gráfico da função .
Sendo:
Seu gráfico será:
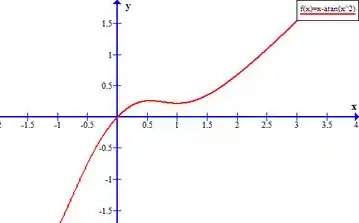
Podemos ver que raiz real da função é:
Passo 3
Agora vamos para a primeira derivada, também usando um programa computacional, obtemos:
E seu gráfico será:
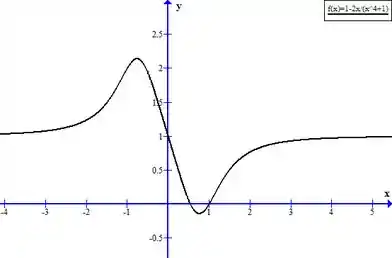
As raízes reais de são:
Para encontrar intervalos crescentes e decrescentes, temos que analisar a primeira derivada da função, onde:
Vamos usar o gráfico e a definição acima para encontrar os intervalos crescentes e decrescentes:
Podemos observar pelo gráfico que a função é crescente:
E decrescente:
Passo 4
Para encontrar estes pontos, temos que conhecer as raízes de e avaliar se há troca de sinal de
Ou então avaliar o sinal da segunda derivada nas raízes de
Vamos então calcular a segunda derivada de
Suas raízes valem:
Plotando o gráfico, temos:
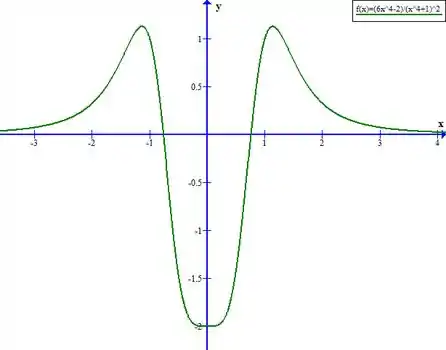
Checando então nas raízes de
Passo 5
Para analisar a concavidade da função e achar seus intervalos, devemos usar a segunda derivada da função.
Pontos de inflexão ocorrem na mudança de concavidade.
Vamos então usar os gráficos e a equação para ajudar a achar a concavidade. As raízes e as assíntotas podem ajudar a identificar:
Suas raízes valem:
Analisando os intervalos:
Logo, os intervalos são:
Resposta
A função é:
Crescente:
E decrescente: