Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.7 - Ex. 37
Um pedaço de fio com de comprimento é cortado em duas partes. Uma parte é dobrada no formato de um quadrado, ao passo que a outra é dobrada na forma de um triângulo equilátero. Como deve ser cortado o fio de forma que a área total englobada seja: (a) máxima? (b) mínima?
Passo 1
Opa, bora pra mais uma questão?! O enunciado nos diz que um pedaço de fio com de comprimento é cortado em duas partes. Uma parte é dobrada no formato de um quadrado e a outra é dobrada na forma de um triângulo equilátero.
Sabendo disso, ele pergunta como deve ser cortado o fio de forma que a área total seja máxima e mínima.
Bem, pra resolver essa questão vamos precisar escrever uma expressão de área total, onde:
Essa expressão deverá ser escrita em função das dimensões fio. Para achar os valores de máximo e mínimo a gente vai calcular . Vamos colocar a mão na massa?!
Passo 2
A área total pode ser escrita como:
Vamos desenhar um esquema com as informações do enunciado:
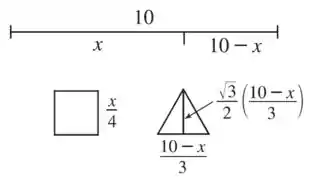
O perímetro do quadrado é , então cada lado deverá medir . Já o perímetro do triângulo equilátero deve ser , então cada lado vai medir . Já a sua altura é dada por:
Então, substituindo :
Substituindo na fórmula da área:
Chegamos em:
Passo 3
O exercício quer a área total máxima e mínima dessas figuras, então vamos calcular :
Fazendo o mmc:
Calculando as raízes temos:
Passo 4
Como pode variar entre zero e dez, substituímos e os extremos do intervalo pra ver quais são os pontos máximos e mínimos:
Substituindo:
Com isso podemos chegar a seguinte conclusão:
Item (a): área máxima encontrada acontece quando , e vale , ou seja, toda a corda é usada para o quadrado.
Item (b): área mínima encontrada acontece quando , e vale .
Resposta
Item (a): área máxima: .
Item (b): área mínima: .