Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 1.4 - Ex. 29
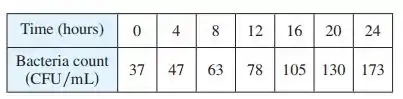
Um pesquisador está tentando determinar o tempo necessário para a população da bactéria Giardia Lamblia dobrar. Ele inicia uma cultura em uma solução de nutrientes e faz a contagem das bactérias a cada quatro horas. As informações são mostradas na tabela.
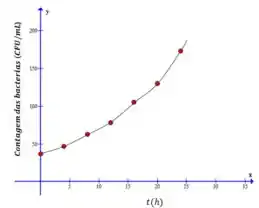
a) Faça um gráfico com os pontos da tabela.
b) Use uma calculadora de gráfico para encontrar uma função exponencial que modele a população de bactérias após horas.
c) Faça um gráfico do modelo da letra b) junto com os pontos da letra a). Use o gráfico para estimar o tempo necessário para as bactérias dobrarem.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
Bom... a questão nos dá a seguinte tabela que relaciona o crescimento de uma população de bactérias no decorrer do tempo:
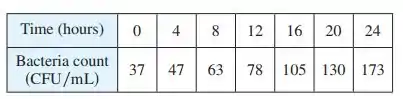
A questão quer que esbocemos o gráfico a partir dos pontos dados nessa tabela. Depois, com auxílio de uma calculadora gráfica, queremos encontrar uma função exponencial do tipo , onde e são constantes, que modele a população de bactérias após horas.
Por fim, devemos plotar o novo gráfico a partir da função que a gente descobrir a fim de estimar o tempo necessário para as bactérias dobrarem.
Então, o que nós vamos fazer é colocar o tempo no eixo horizontal do plano cartesiano, a contagem de bactérias no eixo vertical e marcar os pontos dados na tabela. Depois, vamos colocar esses pontos em um software para encontrar e esboçar a curva da função exponencial que é descrita nessa relação. E usando esse gráfico, vamos observar o ponto onde a população de bactéria é o dobro do número inicial e determinar o valor de nesse ponto.
Vamos lá!
Passo 2
Vamos começar resolvendo a letra (a). Primeiramente vamos selecionar os pontos dados na tabela e marca-los no plano cartesiano:
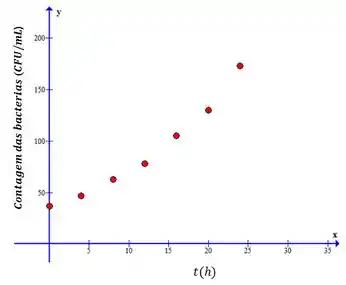
Agora, como a gente aprendeu no jardim de infância, vamos cobrir os pontos haha:
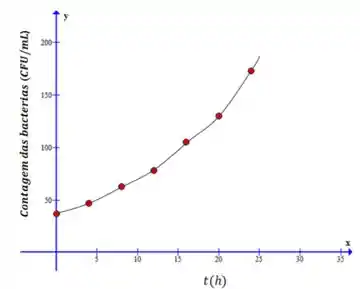
Passo 3
Na letra (b), devemos usar uma calculadora de gráfico para encontrar uma função exponencial na forma que modele a população de bactérias após horas.
Então, a calculadora ou software gráfico vai calcular os valores das constantes e a partir dos pontos fornecidos pela tabela e nos dá a função exponencial:
Passo 4
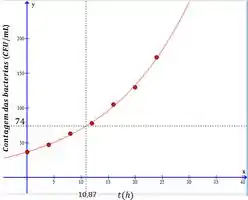
Traçando a curva descrita por essa equação junto com os pontos dados no gráfico do item (a), temos:
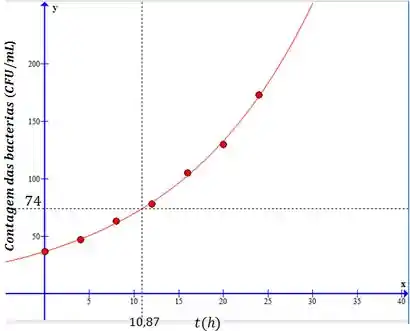
A tabela e o gráfico nos dizem que o número de bactérias inicial é , então elas vão dobrar quando esse número for igual a . Observando o gráfico, nós vemos que para , temos . Então, esse é o tempo necessário para as bactérias dobrarem.
Valeu, galera! Até a próxima! 😉
Resposta
