Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 1.5 - Ex. 11

Uma função é dada por uma tabela, gráfico, formula ou descrição verbal. Determine se a ela é um-pra-um.

g x = 1 - sin ⁡ x

Passo 1

E aí, tudo bem?! Temos a função:

g x = 1 - sin ⁡ x

E queremos saber se ela é um-pra-um. De acordo com o livro, uma função um-pra-um é aquela que nunca repete os valores de y para x diferentes, isto é:

f x 1 ≠ f x 2        

Sempre que:

  x 1 ≠ x 2

Pra a gente resolver esse problema a gente vai primeiro verificar se a função f x = sin ⁡ x é um-pra-um. Depois a gente vai fazer transformações na função f x para chegar em g x e assim analisar a resposta!

A gente vai fazer dessa forma pois a função sin ⁡ x é mais conhecida e mais fácil de esboçar!

Passo 2

Bom, vamos dar uma olhada no gráfico do sin ⁡ x :

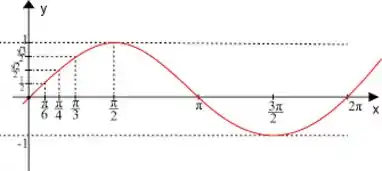
Reparem que:

s e n 0 =   s e n π = 0

Então a função sin ⁡ x não é um-pra-um. Mas e a nossa função:

g x = 1 - sin ⁡ x

Passo 3

Pra a gente sair de f x =   sin ⁡ x   e chegar em 1 - sin ⁡ x a gente precisa multiplicar g x por menos 1 e depois somar 1 . Multiplicando por - 1 temos:

- s e n 0 =   - s e n π = 0

Agora somando 1 :

- s e n 0 + 1 =   - s e n π + 1 = 1

Ou seja, temos que:

g 0 = 1 - sin ⁡ 0 = 1

g π = 1 - sin ⁡ π = 1

Temos dois valores de x para o mesmo   y . Portanto, ela NÃO é uma função um-pra um.

Resposta

A função não é um-pra-um.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o valor exato da função s e c (pi) .
Determine o valor exato da função t g ((1)/(3) pi) .
Determine o valor exato da função t g ((1)/(4) pi) .
Determine o valor exato da função c o s e c ((1)/(2) pi) .
Determine o valor exato da função s e n ((4)/(3) pi) .