Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 8.3 - Ex. 8
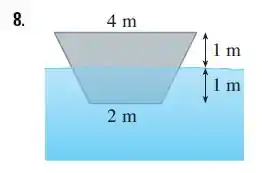
Uma placa vertical é imersa (ou parcialmente imersa) na água e tem a forma indicada nas figuras a seguir. Explique como aproximar a força hidrostática em um lado da placa usando uma soma de Riemann. Então expresse a força como uma integral e calcule-a.
Passo 1
Vamos com muita calma aqui, antes de começar vamos desenhar novamente este trapézio, onde a é a largura do triângulo menor formado e representa o nível da água até a faixa horizontal que é aproximada por um retângulo com altura e largura
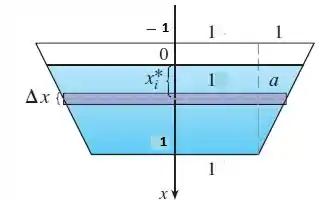
O desenho não está com a dimensão muito boa, mas não se preocupem com isso.
Temos dois triângulos sendo formados de cada lado do trapézio. Se usarmos a semelhança de triângulos obtemos:
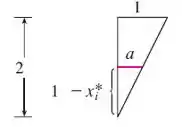
Sendo assim:
Achamos o e vamos deixar ele quietinho ai!
Passo 2
Agora vamos achar a largura . Nós dividimos o retângulo em dois na figura, certo?
O retângulo em questão terá o comprimento 1+a, isso em cada um dos lados do eixo. Então:
Já sabemos o a:
Se chamarmos de área da faixa representada:
Substituindo a largura:
Mas não é isso que queremos, nós queremos a força hidrostática agindo nesta i-nésima faixa que desenhamos:
Sabendo que:
Então:
Somando essas forças e tomando o limite quando , obtemos a força hidrostática total na barragem:
Transformando isso em uma integral, e lembrando que o bloco está submerso apenas de 0 até 1:
Passo 3
No Passo 3 vamos resolver esta integral. Começando pela remoção das constantes:
Sabendo que
Separando os termos:
Agora é só resolver:
Aplicando o intervalo:
Finalizando: