Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 8.3 - Ex. 12

Um caminhão transporta leite com uma densidade de 64,6   l b / p é 3 em um tanque cilíndrico com 6 pés de diâmetro.

  1. Encontre a força exercida pelo leite em uma extremidade do tanque quando o tanque está cheio.
  2. E se o tanque estiver pela metade?

Passo 1

Vamos escolher os eixos de modo que a origem seja o centro do tanque. Então, o círculo tem uma equação simples, x 2 + y 2 = 9 .

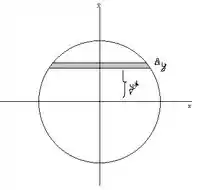
Da equação do círculo, vemos que o comprimento da i-ésima faixa é 2 9 - y i * 2 e assim sua área é:

A i = 2 9 - y i * 2 ∆ y

A pressão nessa faixa é aproximadamente

δ d i = 64,6 ( 3 - y i * )

Passo 2

A força total é dada por:

F = lim n → ∞ ⁡ ∑ i = 1 n 64,6 ( 3 - y i * ) 2 9 - y i * 2 ∆ y

F = 129,2 ∫ - 3 3 3 - y 9 - y 2 d y

F = 129,2 ⋅ 3 ∫ - 3 3 9 - y 2 d y - 129,2 ∫ - 3 3 y 9 - y 2 d y

F = 387,6 ⋅ 1 2 π 3 2 - 0

F = 1744,2 π ≈ 5480   l b

Passo 3

Se o tanque está meio cheio, a superfície do leito está em y = 0 , então a pressão na faixa é δ d i = 64,6 ( 0 - y i * ) . O limite superior de integração moda de 3 para 0 e a força total é:

F = 129,2 ∫ - 3 0 0 - y 9 - y 2 d y = 129,2 1 3 9 - y 2 3 2 - 3 0

F = 129,2 9 - 0 = 1162,8   l b

Resposta

  1. F = 5480   l b ;
  2. F = 1162,8   l b .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma placa vertical é submersa (ou parcialmente submersa) em água e tem o formato indicado. Explique como aproximar a força hidrostática contra um lado da placa por uma soma de Riemann. Então expresse
5. Uma placa vertical é imersa (ou parcialmente imersa) na água e tem a forma indicada na figura a seguir. Explique como aproximar a força hidrostática em um lado da placa usando uma soma de Riemann.
Uma placa vertical é imersa (ou parcialmente imersa) na água e tem a forma indicada na figura a seguir. Explique como aproximar a força hidrostática em um lado da placa usando uma soma de Riemann. Ent
9. Uma placa vertical é imersa (ou parcialmente imersa) na água e tem a forma indicada na figura a seguir. Explique como aproximar a força hidrostática em um lado da placa usando uma soma de Riemann.
Uma placa vertical é imersa (ou parcialmente imersa) na água e tem a forma indicada nas figuras a seguir. Explique como aproximar a força hidrostática em um lado da placa usando uma soma de Riemann. E