Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.3 - Ex. 2
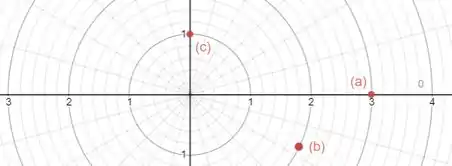
Plote o ponto cujas coordenadas polares são dadas. Então encontre dois outros pares de coordenadas polares desse ponto com e outro com .
a) b) c)
Passo 1
Opa!! Tudo tranquilinho?? A questão pede para plotarmos os seguintes pontosem coordenadas polares:
a)
b)
c)
Lembre-se que a primeira coordenada fornece o raio e a segunda, , o ângulo polar.
Com isso, precisamos ter em mente que o plano polar é dado da seguinte forma:
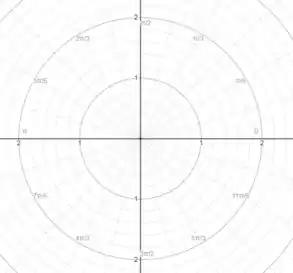
Onde essas circunferências tem raio . Com isso, se , basta girarmos no sentido anti-horário no ângulo para encontramos o ponto desejado!
Caso contrário, se , basta girarmos no sentido horário!!
Também queremos encontrar dois outros pares de coordenadas polares desse ponto com e outro com .
Para o primeiro caso basta somar ao ângulo dado e, para o segundo caso, basta somar a fim de rebater para o quadrante oposto!!! 😉
Agora bora lá!! 😉
Passo 2
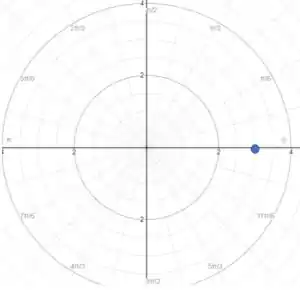
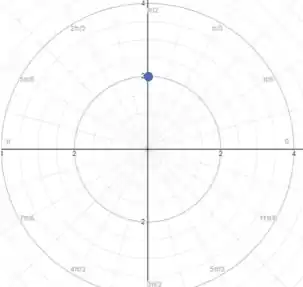
Assim, para o primeiro ponto, , de modo que ele deve estar sobre a circunferência de raio .
Além disso , ou seja, a origem do ângulo.
Com isso, marcando o ponto no nosso plano, temos:
Passo 3
Assim, para o segundo ponto, , de modo que ele deve estar sobre a circunferência de raio .
Além disso . Assim, vamos girar num ângulo de no sentido horário.
Com isso, marcando o ponto no nosso plano, temos:
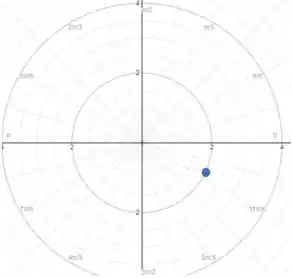
Observação: Também poderíamos partir do sentido anti-horário, mas percorrendo o ângulo .
Passo 4
Por fim, para o ponto , é a mesma coisa de aplicarmos o ponto pois, como ambos estão negativos, é como se estivéssemos “rebatendo” duas vezes entre os quadrantes.
Com isso, marcando o ponto no nosso plano, temos:
A questão pede para plotarmos os pontos dados em coordenadas polares. A primeira coordenada fornece o raio e a segunda o ângulo polar.
Com isso, podemos resumir os nossos pontos na seguinte figura:
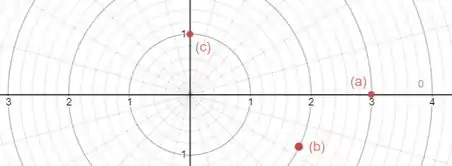
Passo 5
O exercício também pede para descrevermos esses pontos com outras coordenadas polares. O jeito mais fácil de fazer isso é adicionar no ângulo polar:
Uma outra forma de se fazer isso é mudar o sinal de e rebater o ângulo para o quadrante oposto. Para rebater o ângulo para o quadrante oposto basta somar :
Resposta
