Enunciado
Cálculo - Dennis G. Zill - Equações Diferenciais - Vol 1- Ed: 3º - Capítulo 5.2 - Ex. 3
Nos problemas 3-6, as figuras dadas representam o gráfico de uma equação de movimento para uma massa em uma mola. O sistema massa-mola é amortecido. Use o gráfico para determinar:
(a) se o deslocamento inicial da massa está acima ou abaixo da posição de equilíbrio; e
(b) se a massa parte do repouso, dirigindo-se para baixo ou para cima.
Passo 1
Salve salve, vamos lá?
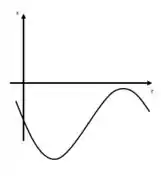
Temos esse gráfico aqui:
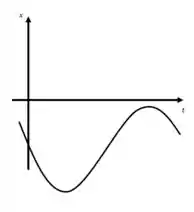
Representando o movimento de uma massa ligada a uma mola. Então temos sua posição em função do tempo
Aí queremos saber:
(a) se o deslocamento inicial da massa está acima ou abaixo da posição de equilíbrio; e
(b) se a massa parte do repouso, dirigindo-se para baixo ou para cima.
Vamos observar o gráfico para ver isso beleza?
Passo 2
Na letra a, queremos saber se o deslocamento inicial, ou seja, está acima ou abaixo da posição de equilíbrio
Cara, analisando o gráfico, a gente vê que em a curva ta pra baixo do . Dessa forma, se é negativo, por referência a gente tem que a posição inicial ta acima da posição de equilíbrio (lembrando que pra cima é negativo e pra baixo é positivo)
Passo 3
Na letra b, temos que saber se a massa parte do repouso, dirigindo-se para baixo ou para cima
Para isso, vamos olhar no gráfico o que acontece instantes após :
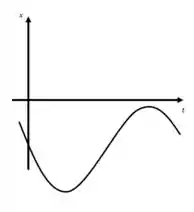
Ó mano, o vai ficando mais e mais negativo nos primeiros instantes
Ou seja: a massa continua se movendo pra cima mesmo depois do start no relógio
Resposta
a) Acima
b) Se movendo para cima