24. Um sistema mola-massa com uma mola dura (Problema 32 da Seção 3.7) sofre a ação de uma força externa periódica. Na ausência de amortecimento, suponha que o deslocamento da massa satisfaz o problema de valor inicial
(a) Seja e gere, em um computador, a solução do problema dado. O sistema exibe batimento?
(b) Faça o gráfico da solução para diversos valores de entre e . Descreva como a solução varia quando aumenta.
Passo 1
Poxa vida, vamos trabalhar aqui com EDO não linear:
Por causa desse , saca?
INFELIZMENTE, resolver uma equação não linear de forma algébrica, como fazemos sem grandes mistérios com as EDO’s lineares, é muito difícil (isso se não impossível). Como o problema já nos dá uma autorização explicita de que podemos usar o computador, a coisa facilita, né?
Aqui, eu vou utilizar o WOLFRAMALPHA para resolver essa EDO, por dois motivos: é um site gratuito pra muitas aplicações matemáticas e também por que ele é simples de mexer. Mas lembrando de que você pode usar qualquer meio computacional ;)
Passo 2
Jogando WOLFRAMALPHA no Google e entrando na página, basta escrever a equação na barrinha de pesquisa delas do jeitinho que está aqui:
Usando as vírgulas para separar as condições! Perceba que já trocamos o por , como é pedido no problema. Ao dar Enter, o site vai te dar a resposta em gráfico:
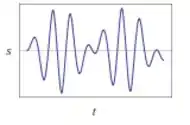
Pela gráfico da resposta, dá pra ver que o sistema exibe sim batimento, afinal ele possui uma envoltória definindo a amplitude da resposta, saca?
Passo 3
Vamos lá, a única diferença desse problema para o da letra A é variação de dentro do cosseno:
Vamos começar substituindo por , onde a gente vai ganhar...
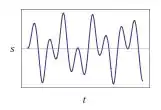
Escolhendo agora ...
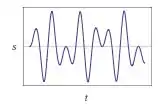
Para ...
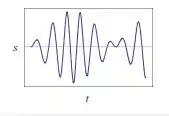
Para ...
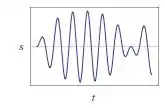
Para ...
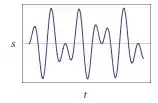
E por último, para ...
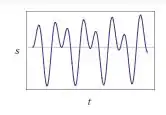
Perceba que à medida que cresce mais próximo do senoidal bonitinha, a gnete vai ganhando .
Resposta
Letra A:
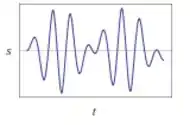
Possui batimento.
Letra B: Desenhos de uma sequência de gráficos com variando de a .