Fala povo, tranquilin? Então, bora lá. Pra começar, em funções compostas, temos:

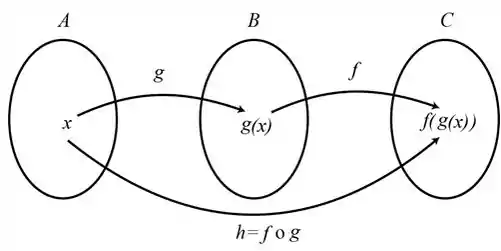
O que em português, significa dizer que os conjuntos serão:

• Domínio de
• Imagem de e Domínio de
• Imagem de

Se for injetora, significa que nenhum elemento de estará associado a mais de um elemento de e se também o for, nenhum elemento de estará associado a mais de um elemento de . Ok, mas e dai? Vamos tentar pensar em caminhos!



Toda vez que eu escolho um único e específico valor de , eu acho um único e específico valor de , incapaz de ser encontrado pra qualquer diferente. Ao usar esse valor de dentro de , ou seja, ao fazermos , já que é injetora, vou acabar encontrando também um único e específico valor de , incapaz de ser encontrado pra qualquer diferente.



Passo 2

Beleza povo, agora olha o seguinte. Temos que provar:

O primeiro passo pra provar isso é inverter a ponta de todas as setinhas da primeira imagem do passo anterior. Olha como fica:



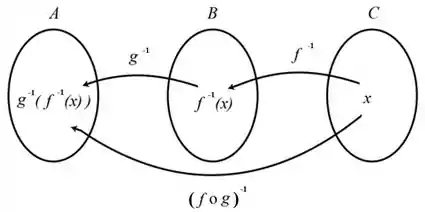
O que significa que os conjuntos, que antes eram:

• Domínio de
• Imagem de e Domínio de
• Imagem de

Se tornarão:

• Imagem de
• Imagem de e Domínio de
• Domínio de

E galera, ao invertermos a ponta das setinhas, podemos compor usando os conjuntos invertidos, e logo as funções inversas! Só de inverter as setinhas e de descrever os conjuntos já tamos provando o que o enunciado pede, afinal a ordem de quem compõem quem mudou, agora temos dentro de , quando antes tínhamos dentro de . Mas se quisermos explicar por caminhos:

Usando um único e específico valor de pertencente a , eu acho um único e específico valor de , incapaz de ser encontrado pra qualquer diferente. Ao usar esse valor de dentro de , ou seja, ao fazermos , já que é injetora, vou acabar encontrando também um único e específico valor de , incapaz de ser encontrado pra qualquer diferente.