Prove que:
Passo 1
Eai povoooo, tranquilão? Olha só, vamos primeiro tentar provar:
E pra isso, vamos olhar o círculo trigonométrico:
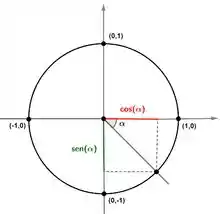
Como tamos começando a questão com função arcosseno, vamos chamar então, na figura acima:
Pois dessa forma, temos que:
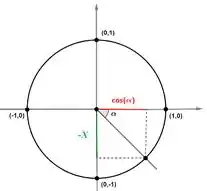
Show de bola. Só que nota o seguinte, se quisermos ver o ângulo , teríamos:
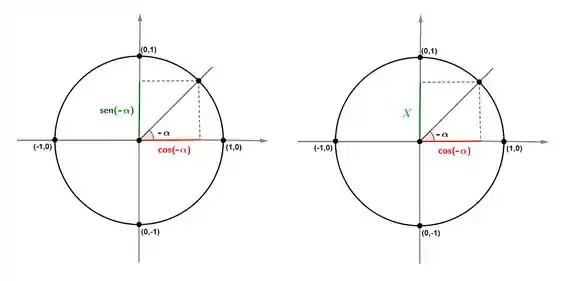
Galerinha bonita, comparando as imagem, podemos ver que, de fato, vale a equação abaix:
Como chamamos “”, se substituirmos, ficamos com:
E fazendo a inversa trigonométrica:
Opa, tamos quase! Já que confirmamos no início da questão “”, substituindo ali do lado esquerdo, temos:
Tá provado!
Passo 2
Vamos provar agora
Pra isso pessoal, a ideia vai ser parecida, ok? Seja o círculo trigonométrico, considerando as tangentes agora:
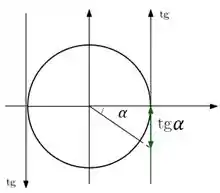
Podemos começar chamando:
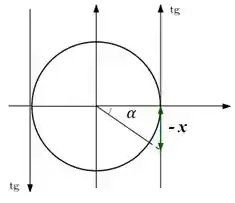
De forma que:
E olhando para o ângulo agora, vemos que:
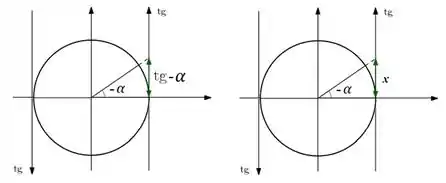
Fazendo a trigonométrica inversa correspondente, temos:
E igualando as duas expressões de que encontramos, fechamos a questão!
Resposta
Provado ao longo dos passos e