Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.5 - Ex. 50
Se , prove que não existe, mas o gráfico de é côncavo para cima em toda parte.
Passo 1
Para começar vamos determinar a concavidade do gráfico. Esta concavidade pode ser determinada pela derivada segunda da função nos valores de x.
Devemos lembrar que:
Então:
Derivando:
A derivada primeira da função indica a inclinação da reta tangente àquele ponto. Sabendo que:
Lembrando que, para o limite bilateral existir os limites laterais direito e esquerdo devem ser iguais.
Ou seja, há uma reta tangente vertical que passa sobre o ponto .
Analogamente:
Passo 2
Analisando a direção da concavidade:
Como a é positiva para rodos os valores de x, o gráfico é côncavo para cima em todos od pontos.
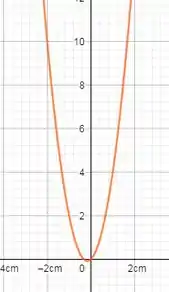
Desenhando o gráfico da função para comprovarmos o que foi visto:
Resposta
Ei, a resposta está no passo a passo :)