Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 9.3 - Ex. 2b
Esboce o gráfico de cada uma das funções do exercício anterior.
b)
Passo 1
Galera, nesse exercício nós temos que esboçar o gráfico da função que nós estudamos no item b) do exercício 1.
Para que você não tenha que voltar lá, nós chegamos nas seguintes conclusões sobre a função :
Côncava para cima no intervalo ;
Côncava para baixo no intervalo ;
Ponto de inflexão quando .
Passo 2
Agora, basta escolhermos alguns pontos de para a função e esboçarmos o gráfico que chegaremos em algo mais ou menos assim:
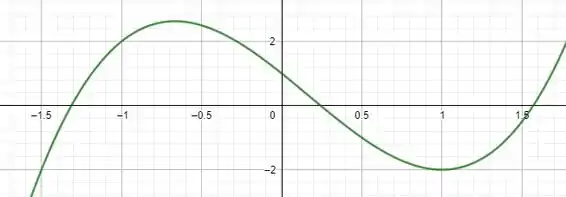
Note que as conclusões apresentadas como revisão do exercício 1 estavam corretas.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Se f for crescente em um intervalo 0 ,b , segue da Definição 4.1 . 1 que f 0f x com qualquer x do intervalo 0 ,b . Use esse resultado nesses exercícios.Use um recurso gráfico computacional para fazer
Se f for crescente em um intervalo 0 ,b , segue da Definição 4.1 . 1 que f 0f x com qualquer x do intervalo 0 ,b . Use esse resultado nesses exercícios.Use um recurso gráfico para fazer uma conjectura
Em cada parte, esboce uma curva contínua y=f ( x ) com as propriedades indicadas:(b) f ( 2 )=4 ,f ' ' ( x )0 com x2 ,f ' ' ( x )0 com x2 , lim x → 2 - f ' x = + ∞ , lim x → 2 + f ' x = + ∞
Em cada parte, esboce uma curva contínua y=f ( x ) com as propriedades indicadas:(a) f ( 2 )=4 ,f ' ( 2 )=1 ,f ' ' ( x )0 comx2 , f ' ' ( x )0 com x2
Em cada parte, esboce uma curva contínua y=f ( x ) com as propriedades indicadas:(c) f ( 2 )=4 ,f ' ' ( x ) 0 com x≠2 , lim x → 2 - f ' x = 1 , lim x → 2 + f ' x = - 1