Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 9.1 - Ex. 35
Questão: 35
Ache a área da região limitada pela curva , pelo eixo x e pela reta .
Passo 1
Em questão desse tipo é bom saber um pouco de gráficos de funções, pelo menos;
1° Encontrar a intersecção da função ln x com o eixo x, beleza?
Qual a condição para que a função ln x passe pelo eixo x? Quando y é zero, certo?
Então seja y = 0 0 = ln x x=1
Agora da pra fazer o gráfico, além disso qual o valor a função assume quando x = e²?
Y = ln e² = 2 , certo? Marque no gráfico.
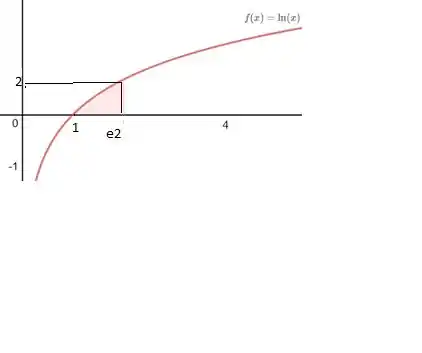
Passo 2
Portanto , veja que o eixo esta limitada logo usaremos integral, note que esse eixo é;
certo, para calcular integração por partes, vamos lá!
Seja f(x) = ln x derivando f(x) =
g’(x) = 1 integrando g(x) = x
= ln x - x dx = x.ln x – x
= 2.e² - e² ( - 1)
=e² + 1.
Resposta
e² + 1.