Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.2 - Ex. 38b
38 – A região no primeiro quadrante limitada em cima pela curva a esquerda pela reta e abaixo da reta é girada em torno do eixo y para gerar um sólido. Determine o volume do sólido pelo:
A – Método da casca.
Passo 1
.
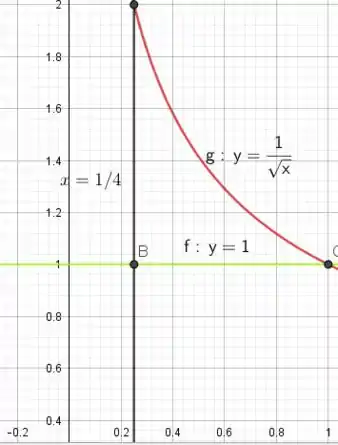
Deste modo temos que nas coordenada de y a figura é limitada
Já para as coordenadas de x ela está limitada em
Passo 2
Resolver em torno do eixo x:
Fórmula:
Inserindo na fórmula teremos:
Resolvendo a integral teremos:
Inserindo os limites de integração, obteremos o volume:
Resolvendo dentro dos colchetes:
Observação: Como pediu o volume e não foi informado uma unidade de medida utilizamos o termo que significa unidade de volume.
Resposta
Exercícios de Livros Relacionados
Nos Exercícios 23-26, use o método da casca para determinar o volume dos sólidos obtidos com a rotação das regiões delimitadas pelas curvas dadas em torno das retas dadas.24 - y = x 3 ,y = 8 ,y = 0 D
Nos Exercícios 23-26, use o método da casca para determinar o volume dos sólidos obtidos com a rotação das regiões delimitadas pelas curvas dadas em torno das retas dadas.24 - y = x 3 ,y = 8 ,y = 0 C
Nos Exercícios 23-26, use o método da casca para determinar o volume dos sólidos obtidos com a rotação das regiões delimitadas pelas curvas dadas em torno das retas dadas.24 - y = x 3 ,y = 8 ,y = 0 A
Nos Exercícios 23-26, use o método da casca para determinar o volume dos sólidos obtidos com a rotação das regiões delimitadas pelas curvas dadas em torno das retas dadas.24 - y = x 3 ,y = 8 ,y = 0 F
Nos Exercícios 23-26, use o método da casca para determinar o volume dos sólidos obtidos com a rotação das regiões delimitadas pelas curvas dadas em torno das retas dadas.25 - y = x + 2 ,y = x 2 C – O