Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.Exercícios Práticos - Ex. 12
Quais são os valores máximo e mínimo da função no intervalo ? Observe que o intervalo não é fechado.
Isso é consistente com o teorema do valor extremo para funções contínuas? Por quê?
Passo 1
Para encontrar podemos encontrar a derivada da função e igualar o resultado a zero para analisar o ponto crítico, caso exista.
Além disso, pode-se também analisar os extremos do domínio da função.
No entanto, a forma mais rápida e fácil de encontrar os valores máximo e mínimo é fazendo o esboço do gráfico da função e encontrar os pontos com esses valores.
Passo 2
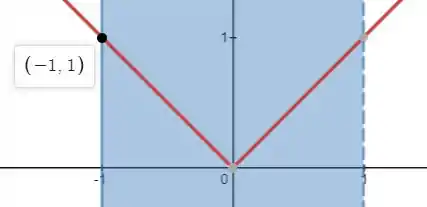
E é possível observar que o máximo absoluto é e o mínimo absoluto é .
Passo 3
Deve-se lembrar que o Teorema do Valor Extremo diz que para a função possuir um valor máximo e um valor mínimo em , então deve ser contínua em um intervalo fechado.
No entanto, ela não diz nada sobre o comportamento de uma função contínua em um intervalo meio aberto e meio fechado como o intervalo dado . Portanto, ele não contradiz o teorema.
Resposta
Sim.