Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.6 - Ex. 34
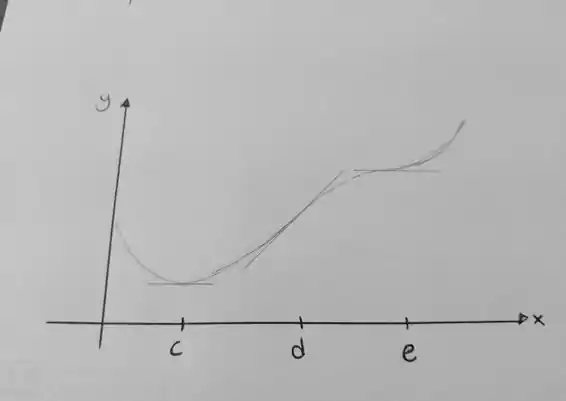
Faça um esboço do gráfico de uma função que passa pelos pontos , , , se as condições dadas forem satisfeitas. Trace também um segmento da reta tangente em cada um desses pontos, se houver uma reta tangente.
Suponha que e que seja contínua em algum intervalo contendo, e .
Passo 1
Vamos com bastaaaante calma aqui nessa questão.
Muita informação que temos que entender. Aqui temos que analisar extremos relativos e pontos de inflexão.
Vamos começar olhando as primeiras derivadas em cada um dos pontos, para identificar os pontos críticos.
Aqui temos
Os pontos críticos, porque neles a derivada é
Passo 2
Agora, vamos classificar esses pontos
Para isso vamos olhar a segunda derivada em cada um deles, que vai ser exatamente o que está aqui embaixo, mas só vale para os pontos críticos
Se ou não existir, não funciona o test
Como
Temos:
Logo é um ponto de mínimo relativo
Em ele disse que
Então o teste da segunda derivada não funciona aqui. Olhando a mudança de sinal da segunda derivada, vemos que ele muda de sinal em , então, apesar dele ser um ponto crítico, na verdade será um ponto de inflexão.
Passo 3
Vamos olhar agora o ponto de inflexão. Que é o ponto onde a segunda derivada muda de sinal.
Isso vai acontecer exatamente em e em
Então esses são os nossos pontos de inflexão.
Passo 4
Para esboçarmos o gráfico, devemos colocar todas essas informações em uma tabela para nos organizarmos
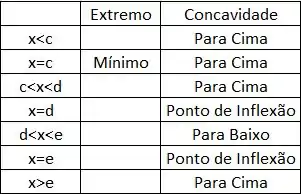
Não podemos esquercer da derivada de e
Que é a inclinação da reta tangente.
O esboço vai ficar:
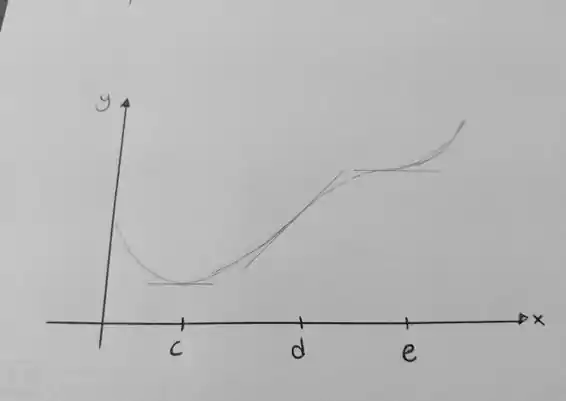
Resposta
