Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 9.4 - Ex. 14c

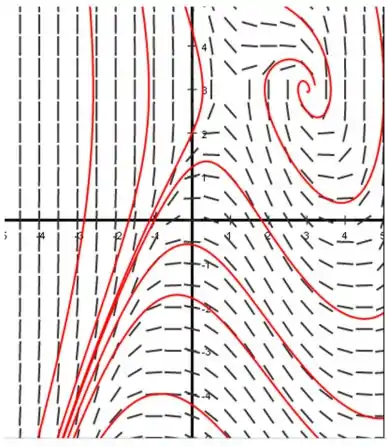
Seja α = 2. Classifique cada ponto crítico investigando o sistema linear correspondente. Desenhe um retrato de fase em um retângulo contendo os pontos críticos..

Passo 1

Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para encontrarmos os valores críticos das equações e achar o equilíbrio. Parece muita coisa, mas é tranquilo. Partiu??

Passo 2

Ok, nosso primeiro passo vai ser determinar quais os pontos críticos, ou seja, igualar as derivadas a zero.

d x d t = 0

d y d t = 0

Oque nos leva a:

y = 3 2 α

y =   - x 2 + 4 x

Passo 3

Pronto!! Agora é só fazermos umas matemágicas aí pra achar o resultado!!

J = 0 - 1 2 x - 4 1

J 3,3 = 0 - 1 2 1     ∴       r = 1 + i 7 2   ; r = 1 - i 7 2 → p o n t o   d e   e s p i r a l

J 1,3 = 0 - 1 - 2 1     ∴       r =   1   ; r = - 2 → p o n t o   d e   s e l a

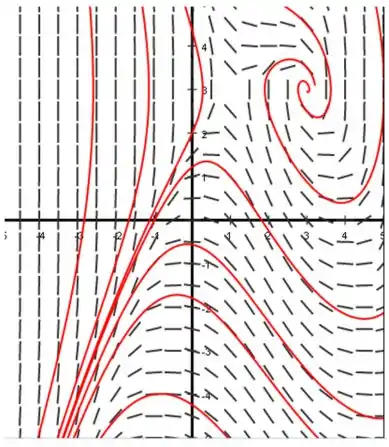
Resposta

J 3,3 = 0 - 1 2 1     ∴       r = 1 + i 7 2   ; r = 1 - i 7 2 → p o n t o   d e   e s p i r a l

J 1,3 = 0 - 1 - 2 1     ∴       r =   1   ; r = - 2 → p o n t o   d e   s e l a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre os pontos críticos.
Esboce as retas de crescimento nulo no primeiro quadrante, como na Figura 9.4.5. Para intervalos diferentes de α, seu esboço pode se assemelhar a partes diferentes da Figura 9.4.5.
Encontre os pontos críticos.
Determine o tipo e as propriedades de estabilidade de cada ponto crítico. Dê atenção especial ao que acontece quando α passa por um ponto de bifurcação.
Esboce as retas de crescimento nulo no primeiro quadrante, como na Figura 9.4.5. Para intervalos diferentes de α, seu esboço pode se assemelhar a partes diferentes da Figura 9.4.5.