Seja f x = cos ⁡ x 2 . a Use um C A S para aproximar o valor máximo de f ' ' x em 0 ,1 . b Qual é o tamanho de n na aproximação do ponto médio de ∫ 0 1 f x d x para garantir que o erro absoluto seja menor do que 5 × 10 - 4 ? Compare seu resultado com o obtido no Exemplo 9 . c Calcule a integral usando a aproximação pelo ponto médio com o valor de n obtido em b .

af ' ' x = 3,845 bn = 18 c∫ 0 1 cos ⁡ x 2 d x ≈ 0,904741

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 7.7 - Ex. 47

Seja .

Use um para aproximar o valor máximo de em .

Qual é o tamanho de na aproximação do ponto médio de para garantir que o erro absoluto seja menor do que ? Compare seu resultado com o obtido no Exemplo .

Calcule a integral usando a aproximação pelo ponto médio com o valor de obtido em .

Passo 1

E aíííí, galerinha! Prontos pra mais um exercício com o Responde Aí?

Bom, para esse exercício em questão, a ideia é bem simples.

Vamos resolver a primeira parte usando um (Sistema Algébrico Computacional) chamado Desmos para nos ajudar a estimar o valor máximo da segunda derivada da função dada.

Em seguida, precisamos estimar o valor de subdivisões para atender a uma precisão específica. Pra isso, temos que nos recordar da fórmula para estimativa do erro absoluto que, para a aproximação pelo ponto médio, é dada por:

Onde e são os intervalos de integração e é o valor máximo da segunda derivada da nossa função (iremos utilizar o valor encontrado na parte ).

Por último, lembrando que a fórmula da aproximação é dada por:

Vamos resolvê-la com o valor de que encontrarmos antes.

Passo 2

Então, derivando a função iremos ter:

E derivando novamente:

Plotando o gráfico dessa função obtida no , conseguimos ver no intervalo no eixo :

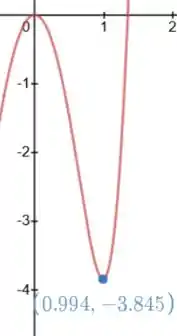
Tal que o valor máximo de é .

Logo:

Passo 3

Agora, vamos calcular o valor de subdivisões da aproximação através de:

Tal que o erro absoluto deve ser menor do que .

Como , teremos:

Ou seja:

E, portanto:

Como deve ter um valor inteiro e par, temos que o menor número de subdivisões será:

Comparando ao resultado do Exemplo , podemos ver que conseguimos diminuir o número de subdivisões necessárias para o cálculo da aproximação pelo fato de termos pego o valor máximo exato de , ao invés de pegarmos o valor inteiro mais próximo acima da curva como feito no Exemplo. Isso nos garante que o tamanho de que encontramos é suficiente para obter a precisão desejada.

Passo 4

Por fim, vamos calcular a integral:

Através do método da aproximação pelo ponto médio. Logo:

Para facilitar o nosso cálculo, vamos montar uma tabela e calcular o valor de cada . Temos, então:

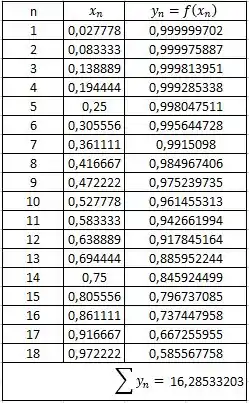
Tal que a aproximação será dada por:

Dessa forma, obtemos:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

(a) Use a Regra do Trapézio e os dados a seguir para estimar o valor da integral. ∫ 1 5 f ( x ) d x (b) Se soubermos que - 2≤f ' ' ( x ) ≤ 3 para todo x, estime o erro envolvido na aproximação na part

Uma tabela de valores de uma função t é dada. Use a Regra de Simpson para estimar ∫ 0 1,6 g ( x ) d x Se 5 t(4) (x) 2 para 0 x 1,6, estime o erro envolvido na aproximação na parte (a).

Usa ( a ) a regra do trapézio, ( b ) a regra do ponto médio e ( c ) a regra de Simpson para aproximar a integral dada com o valor especificado de n . (Arredonde seu resultado para seis casas decimais)