Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 7.7 - Ex. 31

(a) Use a Regra do Trapézio e os dados a seguir para estimar o valor da integral.

∫ 1 5 f ( x ) d x

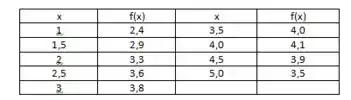
(b) Se soubermos que - 2   ≤   f ' ' ( x ) ≤ 3 para todo x, estime o erro envolvido na aproximação na parte (a).

Passo 1

Para solucionarmos a questão, no trapézio, precisamos calcular o ∆ x . A regra do Trapézio é dada por

∫ a b f ( x ) d x ≈ T n = ∆ x 2 [ f ( x 0 ) + 2 f ( x 1 ) + … + 2 f ( x n - 1 ) + f ( x n ) ]

Onde:

∆ x = b - a n

Então, temos

∆ x = 5 - 1 4

∆ x = 4 4

Logo, ∆ x = 1 .

Aplicando na integral,

T 4 = 1 2 [ f 1 + 2 f 1,5 + 2 f 2,0 + 2 f 2,5 + 2 f 3,0 + 2 f 3,5 + 2 f 4,0 + 2 f 4,5 ]

= 1 2 2,4 + 2 ( 2,9 + 2 3,3 + 2 2,5 + 2 3,6 + 2 3,8 + 2 4,0 + 2 4,1 + 2 3,9 ]

T 4 ≈ 207,2

Passo 2

Estimando o erro envolvido na aproximação na parte (a).

Pela fórmula do limitante de erro | f 4 x | ≤ K , então

| f 4 x | ≤ 3

Então K = 3 . Sendo E s é o erro envolvido no uso da Regra de Simpson, então

E s ≤ 3 b - a 5 180 n 4

Substituindo,

E s ≤ 3 5 - 1 3 180 ( 8 ) 4

E s ≤ 1 2

Resposta

a) T 4 = 207,2

b) E s ≤ 1 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine uma região cuja área seja igual ao limite dado. Não calcule o limite. ∑ i = 1 n 2 n 5 + 2 i n 10
Encontre a área exata da região sob o gráfico de y - e - x de 0 até 2 usando um sistema de computação algébrica para calcular a soma e então o limite no Exemplo 3(a). Compare sua resposta com a estima
Encontre a área exata sob a curva cosseno y = cos ⁡ x de x = 0 até x = b , onde 0 ≤ b ≤ π / 2 . (Use um sistema de computação algébrica para calcular a soma e o limite.) Em particular, qual é a área,
Utilize a Definição 2 para achar uma expressão para a área sob a curva y = x ³ ³ de 0 a 1 como um limite. A fórmula a seguir para a soma dos cubos dos primeiros n inteiros está demonstrada no Apêndice
(a) Expresse a área sob a curva y = x 5 de 0 até2 como um limite. (b) Use um sistema de computação algébrica para encontrar a soma em sua expressão da parte (a). (c) Calcule o limite da parte (a).