Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 7.7 - Ex. 50
Seja
(a) Use um CAS para aproximar o valor máximo de em
(b) Qual é o tamanho de na aproximação de pela regra de Simpson para garantir que o erro absoluto seja menor do que ?
(c) Calcule a integral usando a aproximação regra de Simpson com o valor de obtido em (b).
Passo 1
(a) Vamos usar o Wolfram Mathematica para calcular o valor máximo, em módulo, da quarta derivada de .
Como a gente quer o valor em módulo, vamos maximizar e minimizar a função em , e ver qual é o maior valor em módulo.
Vemos que o maior valor, em módulo, que essa função atinge é . Então podemos dizer que:
Passo 2
(b) Para responder essa, a gente vai usar a fórmulinha:
Sabemos que , e , e queremos garantir que o valor de seja menor que . Então a gente pode resolver a inequação:
Vamos isolar e substituir os valores que a gente conhece:
Como deve ser um inteiro par, o menor número que satisfaz essa inequação é .
Passo 3
(c) Agora é só usar a fórmulinha:
Sendo e :
Onde:
E:
Passo 4
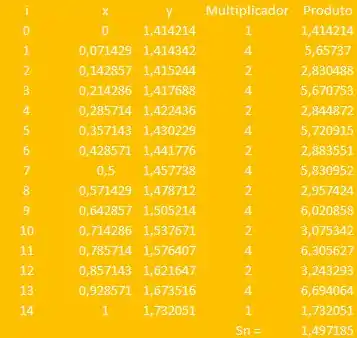
Fazendo variar de até , achamos os valores de e substituímos na fórmula de , para achar:
Resposta
(a)
(b)
(c)