Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 10.2 - Ex. 80

A série no Exercício 6 também pode ser escrita como

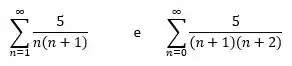
Escreva-a como uma soma começando com (a) n = - 1 , (b) n = 3 , (c) n = 20 .

Passo 1

Olá galerinha, vem fazer esse exercício comigo! Antes de iniciarmos nosso exercício iremos relembrar a série dada no Exercício 6:

5 1 ∙ 2 + 5 2 ∙ 3 + 5 3 ∙ 4 + ⋯ + 5 n n + 1 + ⋯

E do enunciado do nosso exercício temos as seguintes somas:

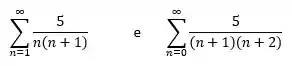
Sendo assim, iremos considerar que:

∑ 5 ( n + x 1 ) ( n + x 2 )

E sabemos que os primeiros termos da série são 1 e 2:

n + x 1 = 1 n + x 2 = 2

Então para n = - 1 , temos o seguinte valor de x 1 :

- 1 + x 1 = 1 → x 1 = 2

E de x 2 :

- 1 + x 2 = 2 → x 2 = 3

Então:

∑ n = - 1 ∞ 5 ( n + 2 ) ( n + 3 )

Passo 2

No item (b) queremos descobrir a soma começando com n = 3 . Sendo assim, para x 1 :

3 + x 1 = 1 → x 1 = - 2

E para x 2 :

3 + x 2 = 2 → x 2 = - 1

Então:

∑ n = 3 ∞ 5 ( n - 2 ) ( n - 1 )

Passo 3

E por fim, no item (c) a soma deve começar com n = 20 . Sendo assim, para x 1 :

20 + x 1 = 1 → x 1 = - 19

E para x 2 :

20 + x 2 = 2 → x 2 = - 18

Então:

∑ n = 2 0 ∞ 5 ( n - 19 ) ( n - 18 )

Espero ter conseguido ajudar, até mais pessoal!

Resposta

  1. ∑ n = - 1 ∞ 5 ( n + 2 ) ( n + 3 ) ;

  2. ∑ n = 3 ∞ 5 ( n - 2 ) ( n - 1 ) ;

  3. ∑ n = 20 ∞ 5 ( n - 19 ) ( n - 18 ) .

Exercícios de Livros Relacionados

Suponha que sum_(k = 1)^(20) a_k = 0 e sum_(k = 1)^(10) b_k = 7 . Determine o valor de sum_(k = 1)^(20) 3 a_k
Expresse as somas nos Exercícios 11-16 em notação sigma. A forma de sua resposta dependerá da sua escolha quanto ao limite inferior do somatório. 1 + 2 + 3 + 4 + 5 + 6
Expresse as somas nos Exercícios 11-16 em notação sigma. A forma de sua resposta dependerá da sua escolha quanto ao limite inferior do somatório. 2 + 4 + 6 + 8 + 10
Escreva as somas nos Exercícios 1-6 sem a notação sigma. Em seguida, calcule-as. ∑ k = 1 4 ( - 1 ) k cos ⁡ k π
Expresse as somas nos Exercícios 11-16 em notação sigma. A forma de sua resposta dependerá da sua escolha quanto ao limite inferior do somatório. 1 + 4 + 9 + 16