Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 10.2 - Ex. 93

A figura abaixo mostra os primeiros cinco quadrados de uma sequência. O quadrado externo tem uma área de . Cada um dos outros quadrados é obtido ligando-se os pontos médios dos lados do quadrado anterior. Calcule a soma das áreas de todos os quadrados.

Passo 1

Oi pessoal! Primeiramente vamos relembrar a teoria de séries geométricas.

As séries geométricas têm a seguinte forma:

Onde e são números reais fixos e . Se , então quando e . A série converge para:

Se , então o primeiro quadrado tem lado:

Utilizando o Teorema de Pitágoras, sabemos que:

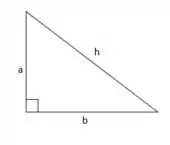
Como o lado do primeiro quadrado tem 2 cm, conseguimos encontrar quanto tem o lado do segundo quadrado:

Ou seja, a área do segundo quadrado é:

Fazendo isso para os próximos quadrados, conseguimos perceber uma sequência:

Passo 2

Sendo assim, podemos observar que nossos quadrados formam a seguinte série geométrica:

Então sabemos:

;
.

E conseguimos calcular a soma das áreas de todos os quadrados:

Tchau galerinha!

Resposta

.

Exercícios de Livros Relacionados

Mostre que o erro ( L-s n ) obtido substituindo-se uma série geométrica convergente com uma das somas parciais s n é a r n / ( 1-r ) .

Para quais valores de r a série 1 + 2 r + r 2 + 2 r 3 + r 4 + 2 r 5 + r 6 ⋯ converge? Encontre a soma da série quando ela converge.

Encontre os valores de x para os quais a série geométrica dada converge. Encontre também a soma da série (como uma função de x ) para esses valores de x . ∑ n = 0 ∞ s e n n x

Curva do floco de neve de Helga von Koch. A curva do floco de neve de Helga von Koch é uma curva de comprimento infinito que engloba uma região de área finita. Para entender a razão disso, imagine que