Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.2 - Ex. 43

Um sólido de revolução é formado quando a região limitada pela curva , pelo eixo e pela reta () gira em torno do eixo . Tome os elementos de área retangulares paralelos ao eixo de revolução e determine o valor de que irá dar um volume de unidades cúbicas.

Passo 1

Essa é uma questão um pouco diferente pois ela não pede para calcularmos o volume diretamente: ele já é dado e precisamos determinar o valor de (que será um limite de integração) para que o volume tenha esse valor (). Além disso, é pedido que usemos elementos retangulares paralelos ao eixo de revolução, então devemos usar o método das cascas cilíndricas (invólucro cilíndrico).

A região que será rotacionada em torno do eixo é

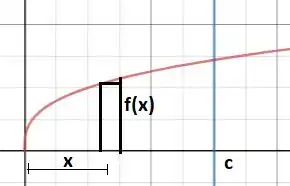
Assim, o volume da região será

onde . Assim,

Passo 2

Fazendo a integração, temos que

Mas sabemos que . Desta forma,

Logo,

Portanto,

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios 23-26, use o método da casca para determinar o volume dos sólidos obtidos com a rotação das regiões delimitadas pelas curvas dadas em torno das retas dadas.24 - y = x 3 ,y = 8 ,y = 0 D

Nos Exercícios 23-26, use o método da casca para determinar o volume dos sólidos obtidos com a rotação das regiões delimitadas pelas curvas dadas em torno das retas dadas.24 - y = x 3 ,y = 8 ,y = 0 C

Nos Exercícios 23-26, use o método da casca para determinar o volume dos sólidos obtidos com a rotação das regiões delimitadas pelas curvas dadas em torno das retas dadas.24 - y = x 3 ,y = 8 ,y = 0 A

Nos Exercícios 23-26, use o método da casca para determinar o volume dos sólidos obtidos com a rotação das regiões delimitadas pelas curvas dadas em torno das retas dadas.24 - y = x 3 ,y = 8 ,y = 0 F

Nos Exercícios 23-26, use o método da casca para determinar o volume dos sólidos obtidos com a rotação das regiões delimitadas pelas curvas dadas em torno das retas dadas.25 - y = x + 2 ,y = x 2 C – O