Suponha que a função de posição de uma partícula em movimento retilíneo seja dada pela fórmula para .
- Use um recurso gráfico computacional para gerar as curvas posição, velocidade e aceleração versus tempo.
- Use um gráfico apropriado para fazer uma estimativa do instante em que a partícula reverte sua direção e, então, encontre esse tempo.
- Encontre a posição, a velocidade e a aceleração no instante em que a partícula reverte sua direção.
- Use os gráficos apropriados para fazer uma estimativa dos intervalos de tempo nos quais a partícula está aumentando e dos intervalos de tempo nos quais está diminuindo sua velocidade e os encontre com exatidão.
- Quando a partícula tem suas velocidades máxima e mínima?
Passo 1
- Para acha a função velocidade é só derivar a função posição, vamos lá:
- Para estimar o instante em que a partícula reverte sua direção temos que analisar a curva da velocidade, e ver onde ela toca o eixo , e isso acontece em .
- Aqui é só aplicar para achar a posição, a velocidade e a aceleração:
- Uma partícula em movimento retilíneo está aumentando sua velocidade quando a velocidade e a aceleração tiverem o mesmo sinal, e diminuindo sua velocidade quando tiverem sinais opostos, vamos analisar isso no gráfico:
- Ela tem suas velocidades máxima e mínima onde a aceleração é igual a zero e no ponto crítico da primeira derivada, assim vamos checar os três valores:
E a função aceleração é a derivada da função velocidade, vamos então derivar:
Pronto, vamos gerar o gráfico das curvas:
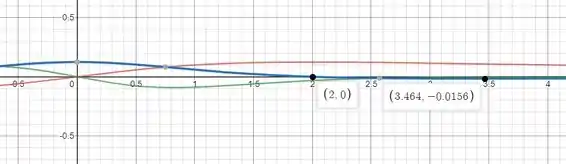
Passo 2
Conseguimos confirmar isso fazendo :
Como nosso intervalo é , temos que em a partícula reverte sua direção.
Passo 3
Passo 4
Temos que está aumentando sua velocidade no intervalo e diminuindo sua velocidade nos intervalos e .
Vamos agora calcular o valor exato, vamos igualar a expressão da aceleração a zero:
Como o intervalo considerado aqui é temos então que , assim a partícula está aumentando sua velocidade no intervalo e diminuindo sua velocidade nos intervalos e .
Passo 5
Pronto, temos então que a velocidade máxima é em e a mínima em .
Resposta
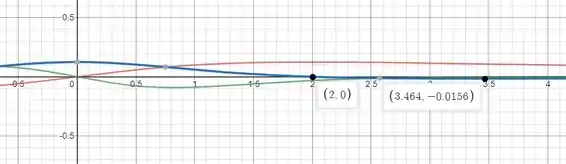
- , e
- A partícula está aumentando sua velocidade no intervalo e diminuindo sua velocidade nos intervalos e
- A velocidade máxima é em e a mínima em