Nestes exercícios, dê as respostas com tantas casas decimais quantas forem permitidas por seu recurso computacional, mas siga o procedimento delineado na caixa Domínio da Tecnologia à página .
Use um recurso gráfico computacional para determinar quantas soluções tem a equação e, então, use o Método de Newton para aproximar a solução que satisfaça a condição dada.
Passo 1
Vamos olhar no gráfico abaixo quantas soluções tem a equação:
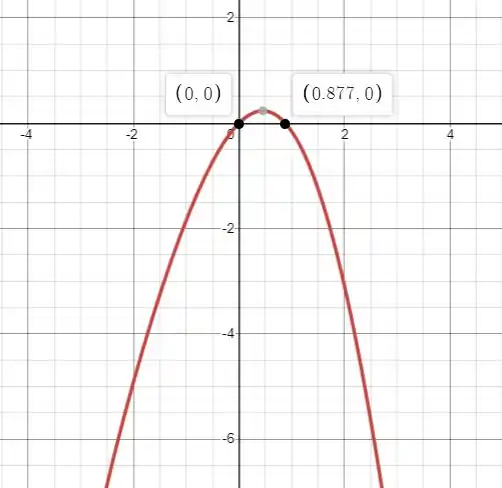
No gráfico notamos que possui duas soluções, vamos agora usar o Método de Newton para aproximar a solução que satisfaça , vamos lá!!
Passo 2
Vamos agora aplicar o método de Newton, para isso vamos usar sua fórmula:
Vamos precisar de , vamos calcular então!!
Ah, e vamos usar a função como:
Passo 3
Para achar a derivada de vamos usar duas regras de derivação, o da função trigonométrica e do polinômio:
Vamos calcular :
Passo 4
Pronto, agora que temos é só jogar na fórmula de Newton:
Vamos agora analisar qual valor usar para , vamos usar , satisfazendo a condição de , pronto, agora é só substituir, vamos lá então:
Vamos continuar usando o método de Newton até o valor de deixar de variar, vamos lá:
Mais uma vez, agora com :
Vamos lá, uma hora acaba, agora :
Vamos achar :
Pronto, o valor não varia mais, então a raiz é .
Resposta
A raiz é .