Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.4 - Ex. 25

Um tanque está cheio de água. Encontre o trabalho necessário para bombear a água pela saída. Nos Exercícios 25 e 26 use a densidade da água igual a 62,5 lb/pé³.

Passo 1

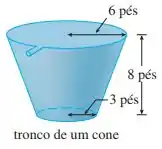
Falaee, belezinha?? Bom... a questão quer que calculemos o trabalho necessário para bombear a água pela saída do seguinte tanque:

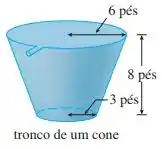
Para isso, a gente sabe que o trabalho é dado por:

W = ∫ a b f ( x ) . d x

Agora vamos aplicar!! 😉

Passo 2

Diremos que x mede a profundidade, em pés, abaixo do bico no topo do tanque.

Um pedaço horizontal de água em forma de disco de ∆ x   p é s de espessura na coordenada x tem raio 3 8 ( 16 - x ) pés, que encontramos por semelhança de triângulo olhando da seguinte forma:

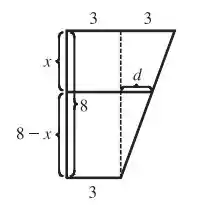
Temos por semelhança que:

d 8 - x = 3 8

Por outro lado:

r = 3 + d

Substituindo d :

r = 3 + 3 8 8 - x ∴

r = 3 8 8 + 3 8 8 - x ∴

r = 3 8 16 - x

Além disso, nosso volume é:

π r 2 ∆ x = π 9 64 16 - x 2   p é s 3

O peso é:

62.5 x   π 9 64 16 - x 2 ∆ x   l b - p é s

e deve ser levantada x pés pela bomba, então a força necessária para bombear a água pela saída é:

62.5 x   π 9 64 16 - x 2 ∆ x   l b - p é s

Passo 3

Nesse sentido, o trabalho total necessário é

W ≈ ∫ 0 8 62.5 x   π 9 64 16 - x 2 d x ∴

W = 62.5 x   π 9 64 ∫ 0 8 x ( 256 - 32 x + x ² ) d x ∴

W = 62.5 x   π 9 64 ∫ 0 8 ( 256 x - 32 x 2 2 2 2 ² + x ³ ) d x ∴

W = 62.5 x   π 9 64 128 x 2 - 32 3 x 3 + 1 4 x 4 0 8 ∴

W = 62.5 9 π 64 11,264 3 ∴

W = 33,000 π ≈ 1.04 × 10 5   l b - p é s

Entendeu direitinho?? Responde aee 😉

Resposta

1.04 × 10 5   l b - p é s .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um tanque está cheio de água. Encontre o trabalho necessário para bombear a água pela saída. Nos Exercícios 23 e 24 use a densidade da água igual a 62,5 lb/pé³.
Mostre como aproximar o trabalho pedido por uma soma de Riemann. Em seguida, expresse o trabalho como uma integral e calcule-a.Um aquário de 2 m de comprimento, 1 m de largura e 1 m de profundidade es
A pressão alta resulta da constrição das artérias. Para manter uma taxa normal de circulação (fluxo), o coração tem de bombear mais forte, aumentando assim a pressão sanguínea. Use a Lei de Poiseuille
Use a Lei de Poiseuille para calcular a vazão em uma pequena artéria humana, tomando ɳ = 0,027ɳ , R = 0,008 cm, l = 2 cm e P = 4000 dinas/cm².