Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.Revisão - Ex. 55

Um tanque cilíndrico está cheio de gasolina com uma densidade de 641   k g / m 3 . Se o eixo do cilindro for horizontal e o diâmetro for de 8   m , ache a força total sobre um extremo devido à pressão do líquido.

Passo 1

A questão pede para calcularmos a força devido a pressão de água em uma placa que tem formato circular com raio 4   m . Vamos usar a equação de circunferência x 2 + y 2 = 16 para modelar essa placa:

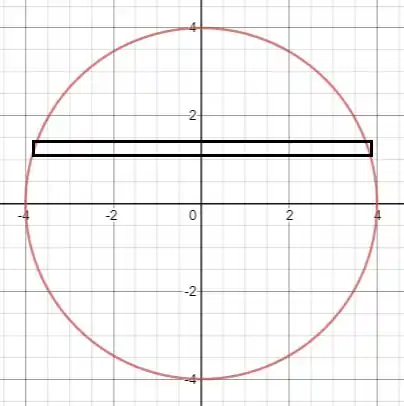
Considerando uma faixa muito fina com espessura Δ y na posição y = y i , temos que a força exercida sobre essa faixa será

Δ F i = p y i   Δ A i ,

onde p ( y i ) é a pressão de água nessa altura e Δ A i é a área da faixa.

Sabemos que a pressão é igual a

p = ρ g ⋅ p r o f u n d i d a d e

Neste caso, temos que a profundidade de água é 4 - y i , de modo que

p y i = ρ g 4 - y i

Já a área será

Δ A i = c o m p r i m e n t o ⋅ Δ y

O comprimento é dado por 2 x i , onde x i 2 + y i 2 = 16 ⇒ x i = 16 - y i 2 . Assim,

Δ A i = 2 16 - y i 2   Δ y

Portanto,

Δ F i = 2   ρ g   4 - y i 16 - y i 2   Δ y

Desta forma, a força resultante será a soma de todos o Δ F i :

F ≈ ∑ i Δ F i = 2   ρ g   ∑ i 4 - y i   16 - y i 2   Δ y

Tomando o limite com Δ y → 0 , temos que a soma vira uma integral:

F = 2 ρ g ∫ - 4 4 4 - y 16 - y 2   d y

Passo 2

Para calcular a força nós vamos quebrar a integral em duas:

F 2 ρ g = 4 ∫ - 4 4   16 - y 2   d y - ∫ - 4 4 y 16 - y 2   d y

Para calcular a primeira integral basta interpretá-la como metade da área de um círculo de raio 4 :

∫ - 4 4   16 - y 2   d y = 1 2 π ⋅ 4 2 = 8 π

Já a segunda é resolvida sem nenhuma conta: note que o integrando é uma função ímpar é o intervalo de integração é simétrico. Isso significa que a integral é 0 .

Desta forma,

F 2 ρ g = 4 ⋅ 8 π - 0 = 32 π

Portanto,

F = 64 π ρ g

Passo 3

Usando ρ = 641   k g / m 3 , g = 9,8   m / s 2 e π = 3,14 temos que

F ≈ 1,26 ⋅ 10 6   N

Resposta

1,26 ⋅ 10 6   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma placa semicircular com um raio de 4m é submersa verticalmente em um tanque com água com seu diâmetro na superfície. Use a fórmula (4) da Seção 6.7 para encontrar a força devido à pressão da água s
Uma placa tem a forma da região limitada pela parábola x 2 = 6 y e pela reta 2 y = 3 e é colocada num tanque com água tendo o seu vértice voltado para baixo e a reta na superfície da água. Ache a forç
A base de uma piscina é um plano inclinado. A piscina tem 2m de profundidade em um extremo e 8m no outro. Se a largura da piscina for 25 m e o comprimento for 40m , ache a força total em decorrência d
Uma placa semicircular com um raio de 3m está submersa verticalmente num tanque de agua com o diâmetro na superfície. Encontre a força decorrente da pressão da agua sobre o lado da placaResolva usando