Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.7 - Ex. 21
A base de uma piscina é um plano inclinado. A piscina tem 2m de profundidade em um extremo e 8m no outro. Se a largura da piscina for 25 m e o comprimento for 40m , ache a força total em decorrência da pressão da agua no fundo
Resolva usando F =
Passo 1
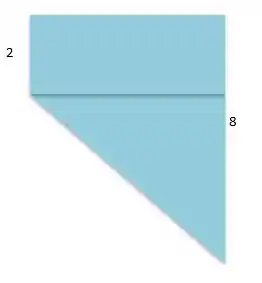Desenhando o problema
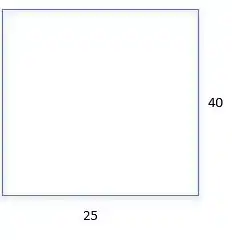
Temos a Figura 1 Mostra a vista de cima da piscina
E a figura 2 mostra um corte da piscina
Queremos a força no fundo
Podemos usar
F =
Sabendo que
da agua = 1000 kg/m³
g = 10m/s²
Passo 2
Logo : F = onde é a altura do objeto mergulhado.
No Nosso caso é o volume de agua = volume do nosso trapezoide.
A do trapézio é (B + b) h/2
(8+2) . 40/2 = 200m²
Volume = 200 . 25 = 5000m³
Passo 3
Calculando F , F =
Sabemos o volume (5000m³ )
Logo
F = 5000.10³.10
Resposta
F =
Exercícios de Livros Relacionados
A face de um reservatório adjacente à agua é inclinado 45º em relação a vertical . A face é um retângulo com 80m de comprimento e um lado inclinado de 40m. Se o reservatório está cheio, ache a força t
A face de um reservatório adjacente à agua é vertical e tem a forma de um trapézio isósceles com 90m no topo e 60 m na base e uma altura de 20 m. Encontre a força decorrente da pressão da agua na face
Uma placa com a forma de triangulo retângulo isósceles é submersa verticalmente num tanque com agua, com um cateto na superfície. Os catetos medem 6 cm cada. Ache A força decorrente da pressão do liqu
Se o extremo de um reservatório de agua tiver a forma de um retângulo e o reservatório estiver cheio, mostre que a medida da força em decorrência da pressão da agua sobre o extremo é o produto da medi
A face de um reservatório adjacente à agua é inclinado 30º em relação a vertical . A face é um retângulo com 50m de comprimento e um lado inclinado de 30m. Se o reservatório está cheio, ache a força t