Uma placa tem a forma da região limitada pela parábola e pela reta e é colocada num tanque com água tendo o seu vértice voltado para baixo e a reta na superfície da água. Ache a força decorrente da pressão de água sobre um lado da paca se a distância for medida em metros.

A questão pede para calcularmos a força devido a pressão de água em uma placa que tem a forma da região limitada pela curva e pela reta :

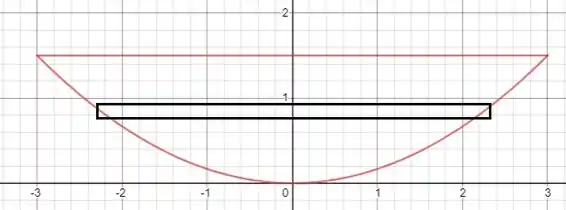
Considerando uma faixa muito fina com espessura na posição , temos que a força exercida sobre essa faixa será

onde é a pressão de água nessa altura e é a área da faixa.

Sabemos que a pressão é igual a

Neste caso, temos que a profundidade de água é , de modo que

Já a área será

O comprimento é dado por , onde . Assim,

Portanto,

Desta forma, a força resultante será a soma de todos o :

Tomando o limite com , temos que a soma vira uma integral: