Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.7 - Ex. 48
A temperatura num ponto de uma bola com condutividade é inversamente proporcional à distância do centro da bola. Encontre a taxa de transmissão de calor através da esfera de raio com centro no centro da bola.
Passo 1
Faaaala galerinha, tudo beleza com vocês!? Vamos nessa!
Nosso objetivo é determina a taxa de transmissão de calor através da superfície , essa superfície é uma bola de raio .
Também sabemos que a temperatura num ponto de uma bola com condutividade é inversamente proporcional à distância do centro da bola.
Vamos começar pessoal! Importante saber que uma bola, nada mais é que uma esfera. Logo, temos:
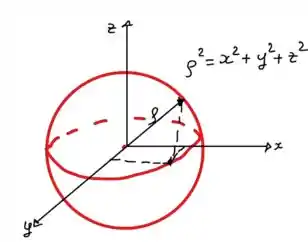
Como a temperatura em um ponto da bola é inversamente proporcional à distância do centro da bola, temos que:
Essa relação que definimos acima, alguns autores acrescentam uma constante , chamada de constante de proporcionalidade. Vamos manter ela, pois não vai interferir nas operações.
Pessoal, se a temperatura em um ponto é dada por , então a taxa de transmissão de calor é dada pelo campo vetorial:
onde é uma constante determinada experimentalmente e é conhecida como condutividade da substância.
E é o gradiente da temperatura:
Assim, a taxa de transmissão de calor através da superfície é dada pela integral de superfície:
Essa integral, podemos reescrever como:
onde é o vetor unitário normal. Ele pode ser definido da seguinte maneira:
Conforme o exemplo do livro, na página , essa é uma possível parametrização da normal para uma esfera.
Agora já temos todas as informações! É só organizar e montar a integral!
Bora lá!
Passo 2
Vamos começar determinando nosso campo :
Como vimos, a distribuição de temperatura pode ser escrita como:
Devemos aplicar o gradiente em :
Fazendo as derivadas em relação a ficamos com:
Assim, podemos escrever o campo vetorial como
Conforme vimos também, o vetor normal a superfície da esfera de raio pode ser escrito como:
Passo 3
Portanto, agora vamos focar em montar a integral:
Substituindo na integral os termos que encontramos no passo anterior, vamos ter:
Note que para os pontos na superfície , nós temos:
Assim, a integral fica:
Repare que todos os termos na integral são constantes. Logo, podemos escrever:
Notem que é a área superficial da esfera, da qual a gente conhece a formula. Que é:
Logo,
Por fim, concluímos que a taxa de transmissão de calor através da superfície é: