Um fluido com densidade e campo de velocidade . Determine a taxa de vazão do fluido saindo da esfera .

Vamos procurar uma parametrização para nossa superfície, que é a de esfera

Só que como o sólido dessa figura é uma esfera então o melhor a se utilizar nessa questão são as coordenadas esféricas, o que nos dá parâmetros iguais a:

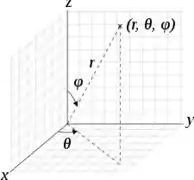
Como a equação da esfera é:

Vemos que nosso raio da esfera é , então nossa parametrização fica:

E assim achamos nosso vetor das equações parametrizadas:

Como temos uma esfera completa, temos todos os valores possíveis para as variáveis:

Agora temos que calcular os vetores e . Calculando as derivadas parciais de:

• Derivada em relação a , tratando como constante:

Ficamos com:

• Derivada em relação a , tratando como constante:

Ficamos com:

Agora fazemos o produto vetorial de por :

Para cada componente e , temos que multiplicar a matriz que achamos tirando a linha e a coluna da componente que estamos procurando. Depois, tiramos o determinante de cada matriz e ficamos com:

O que é a mesma coisa que:

Agora calculamos nosso termo :

Temos que:

E:

Vamos substituir nossos parâmetros em :

Ficamos com:

Dessa forma a fórmula da vazão será:

Substituindo na nossa integral:

Ficamos com:

Tirando a constante pra fora da integral:

Fazendo o produto escalar, multiplicamos cada coordenada do primeiro vetor por sua coordenada correspondente no segundo vetor e somamos tudo. Portanto:

Simplificando:

Como:

Temos:

Agora podemos finalmente resolver nossa integral. Resolvendo essa integral de dentro em nós teremos:

Aplicando os limites de integração:

Agora vamos integrar em . Aplicando a substituição:

Ficamos com:

Voltando para o domínio de temos:

Aplicando os limites:

Então a vazão será: