Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.7 - Ex. 46
Use a Lei de Gauss para encontrar a carga dentro de um cubo com vértices se o campo elétrico é
Passo 1
E aiii minha turminha fera, tudo belezinha com vocês!?
Nessa questão devemos usar a lei de Gauss para encontrar a carga dentro de um cubo de vértices:
Com campo elétrico:
Vamos pensar juntos em uma solução, beleza!
A carga dentro de uma superfície é dada por:
Onde é a permissividade elétrica no vácuo. Mas não se preocupe com ela, vamos manter ela desse jeitinho mesmo.
Aqui podemos dividir em seis partes, que são as seis faces do cubo. Por convenção, aponta para fora.
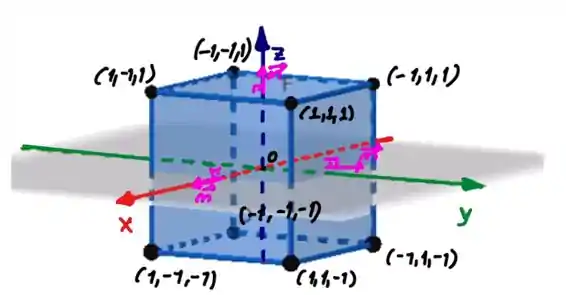
Aqui vamos ter que achar o fluxo que passa por cada face do cubo, e depois somar todos.
Vamos fazer um como exemplo, e para os demais o processo vai ser idêntico. Apenas mudando a direção do vetor norma.
O fluxo através da face do cubo que faz parte do plano . Assim,
Essas integrais acima são equivalentes, o que acontece, é que escrevemos o vetor como:
onde é um vetor normal à superfície .
Portanto, . Pois essa superfície aponta apenas na direção do x positivo.
Note que para todos os pontos, . Logo, temos:
Essa integral acaba sendo a área da face do cubo!
Portanto, o valor é unidades quadradas.
Logo, o fluxo que passa por essa região vale:
Passo 2
Agora vamos analisar outra face.
O fluxo através da face do cubo que faz parte do plano . Assim,
onde é um vetor normal à superfície. Portanto, .
Note que para todos os pontos, .
Essa integral acaba sendo a área da face do cubo também!
Portanto, o valor é unidades quadradas.
Logo, o fluxo que passa por essa região vale:
Passo 3
Agora a gente faz uma pausa e vamos refletir um pouco.
A gente pode observar que ambas a superfície e são simétricas em termos de e . Portanto, o fluxo que atravessa as outras quatro faces do cubo também serão iguais a 4 unidades quadradas. Logo, o fluxo total através do cubo é:
As seis faces vezes o fluxo que passa por uma face. Assim achamos a resposta acima.
Logo, a carga dentro da superfície é
Essa questão não é difícil, mas temos que fazer com calma! Assim conseguimos perceber situações de simetria como essas.