Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.7 - Ex. 44
A água do mar tem densidade e escoa com velocidade , onde são medidas em metros e as componentes de em metros por segundo. Encontre a taxa de vazão para fora do hemisfério
Passo 1
E aiii galera, belezinha!? Vamos nessa!
Vamos entender com calma a questão, beleza!
Precisamos determinar a taxa de vazão de água do mar (com densidade ) que escoa com velocidade para fora do hemisfério:
Galera, quando tratamos de vazões, se soubermos o valor da densidade em qualquer ponto e a velocidade nesse mesmo ponto, a taxa de vazão da substância através de uma superfície pode ser dada por:
onde e é orientada positivamente.
Nessa questão, a densidade da água do mar é e a velocidade de escoamento é . Portanto,
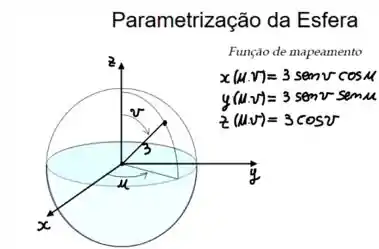
Como se trata de uma esfera de raio 3, podemos ter a seguinte parametrização:
Um ponto de bastante atenção aqui, porque ele deixa claro que quer a parte do hemisfério . Assim, temos que:
Agora já podemos colocar mão na massa! Bora lá!
Passo 2
Vamos começar lembrando da parametrização da esfera.
Onde,
A integral que devemos calcular é a seguinte:
E sabemos que:
Parametrizando , vamos ter:
Notemos que podemos expressar a integral desse jeito:
onde é o vetor unitário normal e .
O fluxo através da superfície é definido somente se a superfície for orientável. Note que se a superfície é orientável, terão dois vetores normais em todos os pontos. Podemos escrever:
Onde, representa um produto vetorial das derivadas parciais de em relação a e .
Passo 3
Agora, vamos calcular as derivadas parciais de .
Calculando o produto vetorial na forma matricial:
Aplicando o determinante vamos ter como resposta:
Logo, é:
Agora é só substituir na integral!
Passo 4
Substituindo na integral, vamos ter:
Resolvendo o produto escalar e simplificando o máximo possível, vamos ter:
O segredo para chegar nessa expressão reduzida, é utilizar a relação trigonométrica a seguir:
Agora nosso objetivo é resolver a integral. Mas antes vamos substituir os intervalos de integração da superfície:
Assim, temos:
Passo 5
Observe que os termos u e v são independentes um do outro. Isso nos permite escrever a integral desse jeito:
Assim, podemos resolver as integrais separadas e simultaneamente. E obtemos a resposta apenas multiplicando o resultado de cada integral.
Um recurso muito utilizado, quando é possível separar as variáveis de integração.
Na primeira integral, devemos fazer uma substituição do tipo:
Para a segunda devemos escrever da seguinte forma:
E substituir pela relação:
Fazendo isso, a integral fica:
A primeira integral esta tranquila de resolver. Já na segunda, vamos ter que separar as integrais e aplicar uma substituição:
Vamos fazer a substituição do tipo:
Agora, ficamos com:
Passo 6
Integrando tudo e voltando para as variáveis e , vamos ter:
Observe uma coisa. Vamos aplicar os limites de integração apenas no primeiro termo, desse jeito:
Resolvendo, temos que:
Repare que deu zero o valor da primeira integral, logo concluímos que o fluxo vai ser zero. Nem precisa a gente aplicar os limites de integração dos demais termos.
A taxa de vazão é igual a: