Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.4 - Ex. 47
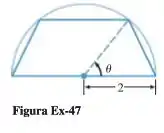
Um trapézio é inscrito em um semicírculo com raio , de forma que um lado está sobre o diâmetro (Figura Ex-47). Encontre a maior área possível para o trapézio. [Sugestão: Expresse os lados do trapézio em termos de .]
Passo 1
Então galera, aqui o que temos que fazer é estabelecer uma equação para a área do trapézio no qual os termos estão em em função de teta. Show! No triângulo formado pelo desenho dado no enunciado podemos gerar um triângulo retângulo, certo? Representando isso, teríamos:
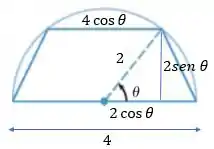
O traço pontilhado vale porque é o raio do semicírculo. Se decompormos essa linha tracejada em e em teremos e , assim como está indicado na figura! Tendo isso em vista, temos que a área de um trapézio é:
No qual é a base maior, é a base menor e é a altura! Substituindo os dados que temos:
Show!
Passo 2
Como queremos a maior área possível para o trapézio, então estamos falando de ponto de máximo. Sendo assim, vamos em busca desse ponto de máximo! Derivando nossa função, teremos:
Como , então:
Igualando nossa derivada a zero:
As únicas formas disso dar zero é se:
Ou se:
Da primeira tiramos que , então . Já da segunda tiramos que , então . No entanto, o nosso intervalo está contido em , pois é a validade das componentes de seno e cosseno que escrevemos! Sendo assim, o único ponto crítico é , além das extremidades do intervalo!
Passo 3
Agora que encontramos o ponto crítico, vamos substitui-lo na nossa expressão da área:
Mas como sabemos que essa é a maior área? Bom, para termos certeza vamos substituir as extremidades na nossa expressão também, se liga:
Sendo assim, podemos concluir que, de fato, a maior área é !