Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 1.4 - Ex. 2
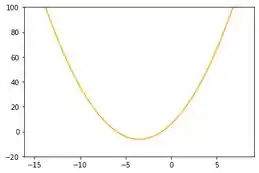
Use uma calculadora gráfica ou um computador para determinar qual das janelas retangulares dadas produz o gráfico mais apropriado da função .
Passo 1
Meus amores, aqui nessa questão a gente tem que fazer vários gráficos, com janelas diferentes e analisar qual é a melhor pra função a seguir:
A janela é o intervalo retangular que vamos mostrar no plano cartesiano. E ela precisa não ser grande demais nem de menos. Mostrar bem a função de forma que a gente entenda o seu comportamento e mostrar pontos importantes, como máximos, mínimos, assíntotas, raízes e vértices.
Essa nossa função aqui é uma função polinomial de segundo grau, ou seja, uma parábola. Então já te adiando que nós precisamos conseguir visualizar isso no gráfico.
Passo 2
Para o intervalo temos o seguinte gráfico. Ele não é bom, ele corta a parábola e ela não tá centralizada. Eu te pergunto, se você não já soubesse que é uma parábola, você conseguiria dizer? Se a resposta for não, então a janela tá bem ruim.
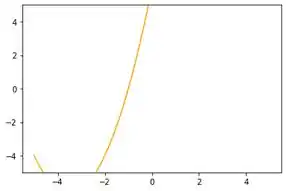
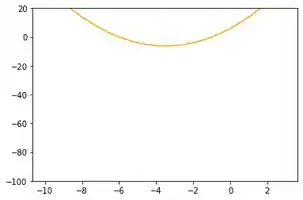
Já para o intervalo vamos ter a visualização a seguir. Com o pensamento que tivemos pra anterior, essa é ainda pior. Se vemos esse gráfico apenas, não fazemos ideia da sua expressão porque estamos vendo apenas um pedacinho da curva.
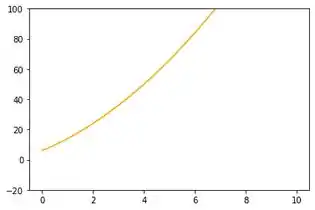
No intervalo de a coisa já muda de figura. Olha que parábola bonita! Toda centralizada no plano, nem grande demais e nem de menos, entendemos tudo! Então isso significa que essa janela é adequada.
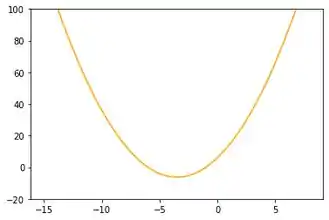
Mas vamos aumentar só mais uma vez pra ver com fica maior. E bem, porque o enunciado pediu rsrs. Por fim, para teremos esta visualização que sobre muuuuito espaço abaixo do ponto mínimo. Isso não é legal, faz a gente ver o gráfico estranho e não faz sentido a gente ver tanto espaço vazio.
Bem acho que deu pra entender o espírito da coisa ne. O que é uma janela boa e o que não é!
Valeu, pessoal ;)
Resposta
Essa é a melhor visualização
