Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 1.4 - Ex. 11
Determine uma janela retangular apropriada para a função dada e use-a para fazer o gráfico da função:
Passo 1
Opa, bora lá! Temos a função:
Temos que definir a janela apropriada e fazer seu gráfico.
Primeiramente, você sabe o que é janela apropriada?
O gráfico vai pegar um intervalo da função, pois não podemos fazer um desenho de a . Então temos que escolher de onde até onde vamos mostrar. E a janela apropriada é o intervalo que mostre os pontos importantes da função (máximos, mínimos, raízes, assíntotas e etc). Em outras palavras, a gente tem que ser capaz de de fato entender o comportamento dessa função. Mas sem ser grande demais também.
Pra isso a gente tem que começar pensando no domínio dessa função, que são os valores que pode assumir. Bom, se a gente olhar pra essa função, a única restrição é aquele denominador que não pode ser nulo, então:
Nesse ponto a função não tá definida, então ele precisa aparecer no gráfico. No passo 2, vamos avaliar o que acontece perto desse ponto e ver também alguns outros pontos de interesse, como as raízes.
Passo 2
A medida que nos aproximamos de zero a gente passa a ter valores muito grandes, positivos e negativos. Com valores muito pertinho de 0, mas positivos, temos:
Com um valor pertinho de zero, mas negativo:
Na notação de limites, temos, pela direita:
E pela esquerda:
Ou seja, a medida que nos aproximamos de pela direita tendendemos a e pela esquerda .
Passo 3
Agora vamos pra próxima preocupação: as raízes! Para zerar essa função devemos ter:
A raiz cúbica de um número negativo é um número negativo:
Bom, as raízes são pontos importantes, então a janela apropriada tem que mostrá-las.
Também existem mais duas raízes, mas elas não são reais!
Passo 4
E se a gente agora pegar um intervalo que mostre esses pontos importantes que achamos, será que fica bom?
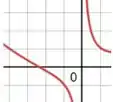
Não parece muito bom! Parece que pode ter muito mais coisa acontecendo fora desse intervalo que a gente não tá conseguindo ver porque ele tá muito pequeno.
Vamos tentar um maior!
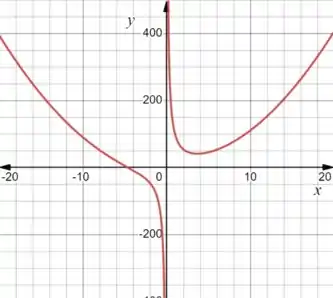
Opa! Esse parece bem melhor. Repara que temos um mínimo ali perto de que a gente não ia ver com aquela janela menor.
Então vamos ficar com a janela de por.
Repara que se ela fosse bem pouquinho maior ou menor, não faria diferença, ela ainda mostraria o comportamento da função. A resposta aqui não é exata, mas queremos uma visualização representativa!