Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 1.4 - Ex. 17
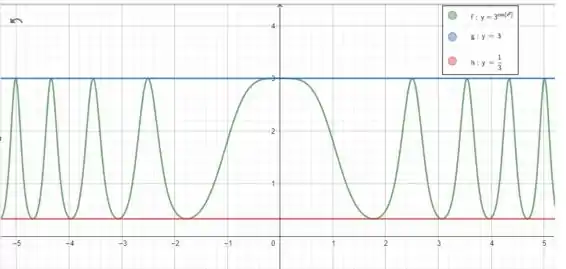
Determine uma janela retangular apropriada para a função dada e use-a para fazer o gráfico da função
Passo 1
Fala galera, tudo bem? Para determinar qual é o intervalo em que veremos essa função, vamos verificar se conseguimos saber sobre sua paridade. Com isso já poderemos analisar o tamanho da base do nosso retângulo: se só no lado positivo, se olhamos nos dois, enfim...
E depois? Depois vamos analisar sua amplitude! Como temos uma função periódica como argumento de uma exponencial, o valor do cosseno vai variando dentro de uma janela, então ver os principais pontos e o que isso representa na função é uma boa ideia também!
E depois? Depois é só plotar o gráfico! Lembrando das principais características das funções básicas.
Beleza? Mas calma, vou fazer passo a passo contigo!
Passo 2
Nossa função
Dizemos que ela é ímpar se
E par se
E não tem paridade definida quando não for nenhuma dessas coisas! Fazendo na função
Podemos verificar por inspeção que a nossa função atende a seguinte condição .
Então, nossa função é par e será simétrica em relação ao eixo e nunca vai atingir um valor negativo
Sendo assim podemos pegar a seguinte janela para o , sendo um intervalo simétrico ao eixo dos .
Passo 3
Agora vamos verificar a amplitude! Como no argumento da função temos um cosseno, e sabemos que ele é limitado, vamos ver quais os valores máximos e mínimos dele, e com o zero:
Vemos que a função atinge seu máximo em e mínimo
De qualquer forma temos um valor positivo para a imagem. E o gráfico fica limitado a esses dois valores! E quando o argumento da função é zero, temos que
Assim verticalmente fica entre , mas podemos ampliar um pouco para observarmos melhor p gráfico e fazer .
Temos uma função exponencial, mas sua imagem fica limitada porque temos uma função limitada no seu argumento
Sendo assim temos o esboço
