Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 1.4 - Ex. 12
Determine uma janela retangular apropriada para a função dada e use-a para fazer o gráfico da função
Passo 1
Oláááá!
Nessa questão, queremos a janela apropriada e o gráfico da seguinte função:
Mas antes de qualquer coisa, você sabe o que é janela apropriada?
Bom, o gráfico vai pegar um intervalo da função, pois não podemos fazer um desenho de a . Então temos que escolher de onde até onde vamos mostrar. E a janela apropriada é o intervalo que mostre os pontos importantes da função (máximos, mínimos, raízes, assíntotas e etc). Em outras palavras, a gente tem que ser capaz de de fato entender o comportamento dessa função. Mas sem ser grande demais também!
Então vamos começar calculando o domínio da função, as raízes e outros pontos que precisam aparecer na nossa janela!
Passo 2
O domínio são os valores que pode assumir. E se a gente olhar pra essa função, a única restrição é aquele denominador que não pode ser nulo, então:
Mas isso já não vai acontecer nunca porque um número ao quadrado é sempre positivo. Então o domínio são todos os reais.
Pra achar as raízes, igualamos a função a zero:
Mas como o denominador não pode ser zero, é o numerador que vamos anular. Então temos uma raiz em:
E esse ponto é importante, então tem que estar contido na janela pra ela ser adequada!
Passo 3
Uma coisa interessante de a gente reparar é que essa função vai ser sempre menor que 1, porque
É verdade pra qualquer valor de . Então a nossa janela não precisa ser maior do que isso na vertical, ela pode ir apenas de ou até menos.
E se a gente fizer a seguinte continha pra
percebemos também que , ou seja, a nossa função é ímpar. Sendo assim, ela vai ser simétrica em relação a origem e devemos pegar para um intervalo simétrico
Passo 4
Então vamos tentar pegar uma janela simétrica, que cubra a origem e que não seja muito grande verticalmente:
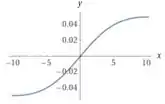
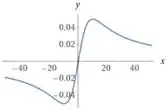
Hmmm, seria interessante a gente ver melhor como é essa função em valores maiores que 10 e menores que -10, muita coisa pode acontecer pra um lado e pro outro. Vamos tentar!
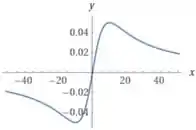
Opa! Agora ficou bom. Conseguimos ver pontos de máximo e mínimo e que ela vai tendendo pra zero conforme cresce ou decresce muito.
Uma janela apropriada é:
Resposta
