Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 3.9 - Ex. 23e
23. Use as definições das funções hiperbólicas para achar os seguintes limites.
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Passo 1
Aqui queremos encontrar o seguinte limite:
A secante é a mesma coisa que 1 sobre cosseno:
A gente sabe que a definição de cosseno hiperbólico é:
Agora vamos usarisso no nosso limite e ver qual resultado vai dar. Aqui também vale a pena a gente lembrar como funciona a função exponencial, vou trazer o gráfico dela aqui:
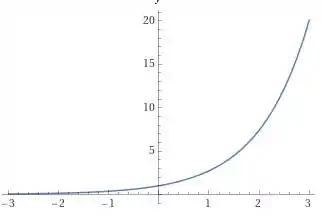
Essa é uma função que vai para infinito quando vai para infinito e que vai para zero quando vai para menos infinito.
Passo 2
Queremos resolver o seguinte limite:
Substituindo a secante pelo inverso do cosseno:
Substituindo a fórmula do cosseno hiperbólico:
Portanto, temos:
Substituindo por infinito:
Resposta
Exercícios de Livros Relacionados
Use as definições de funções hiperbólicas para achar o valor do limite. lim x → ∞ tanh x
Use as definições de funções hiperbólicas para achar o valor do limite. lim x → 0 - coth x
Encontre a derivada.f (x) = e^(cosh 3 x)
Encontre a derivada.f (x) = x coth sqrt(x^2 + 1)
Use as definições de funções hiperbólicas para achar o valor do limite. lim x → 0 + coth x