Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.1 - Ex. 23
Use a equação para responder as questões.
- Com quais valores de vale
- Com quais valores de vale
- Com quais valores de vale
- Tera um valor mínimo? Um valor máximo? Se assim for, determine-os.
Passo 1
Vamos começar com a letra
Vamos fazer bhaskara!!!
Isso da pra gente
Na letra temos
Passando o pro outro lado, temos:
Não podemos ter raiz negativa, então não temos nenhum valor de para
Passo 2
Na letra e vamos fazer uso do resultado da letra , a gente tem duas raízes, e e como nossa equação do segundo grau tem (o termo que acompanha ) positivo, a nossa parábola vai ser virada pra cima, vamos desenhar ela aqui:
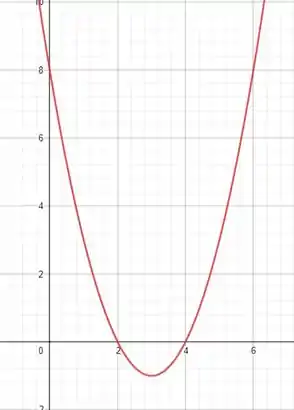
Podemos ver que o acontece quando
Bom, pra letra a gente viu que a função tem um mínimo, vamos calculá-lo fazendo o do vértice, calculado assim
Quando
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Determine o domínio e a imagem da função e desenhe um esboço de seu gráfico. f x = x 2 - 1 , s ex1 2 x + 3 , s e1 ≤ x
Determine o domínio e a imagem da função e desenhe um esboço de seu gráfico. g x = x 3 + 3 x 2 - 4 x - 12 x 2 + x - 6
Determine o domínio e a imagem da função e desenhe um esboço de seu gráfico. F x = x + 3 , s ex- 2 4 - x 2 , s e - 2 ≤ x ≤ 2 3 - x , s e2x
Nos Exercícios 1-4, utilize uma calculadora gráfica ou um computadorpara determinar qual das seguintes janelas de visualização exibeo gráfico mais apropriado da função especificada.4. f x = 5 + 4 x -
Nos Exercícios 5-30, determine uma janela de visualização apropriada para a função dada e a utilize para exibir o gráfico da função.8. f x = x 5 - 5 x 4 + 10