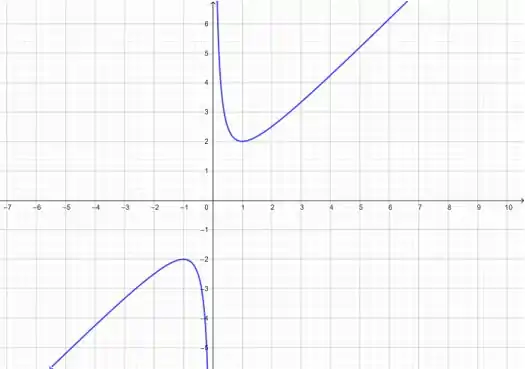
Esboce o gráfico de y = x +(1/x) adicionando as correspondentes coordenadas y nos gráficos de y = x e y = 1/x. Use um recurso gráfico para confirmar que seu esboço está correto.

Então, para esboçar o gráfico, vamos somar os gráficos de e . Para isso, basta imaginar que eles estejam “empilhados” um em cima do outro. Vamos ver isso melhor.

Primeiro, o gráfico de :

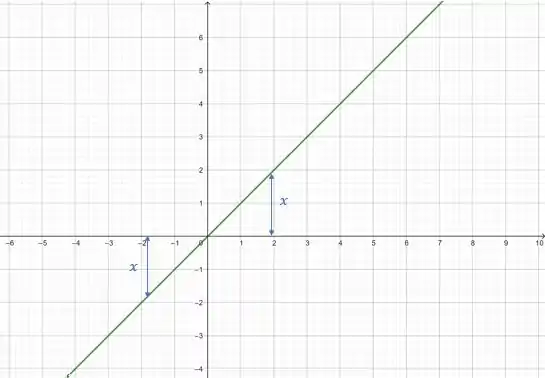
Agora, vamos desenhar o no mesmo sistema:

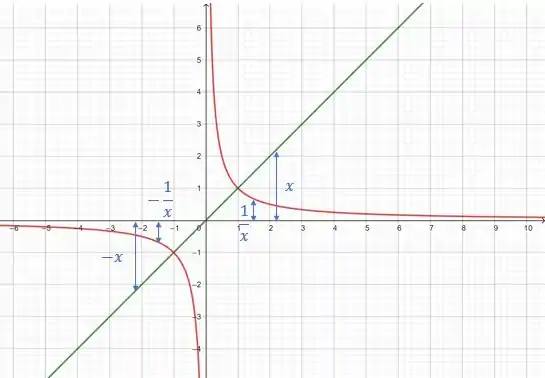
Bom, a distância do eixo até um ponto em é igual a distância do eixo ao . Isso falando de um mesmo ponto, por exemplo , que aí seria a distância de até e até , ou seja, é a distância do eixo até o mesmo ponto.

Com isso, para achar a soma das duas, vamos somar os valores de cada : na parte positiva do eixo , temos que as duas funções possuem valores positivos, então, vai aparecer algo acima delas, pois ocorrerá uma soma de valores positivos!

Já na parte negativa do eixo , as duas funções possuem valores negativos, então, vai aparece algo embaixo das duas, pois elas se subtraem (ficando mais negativo ainda) nesse lado do gráfico.

Dessa forma, soma das duas vai aparecer assim (em azul):

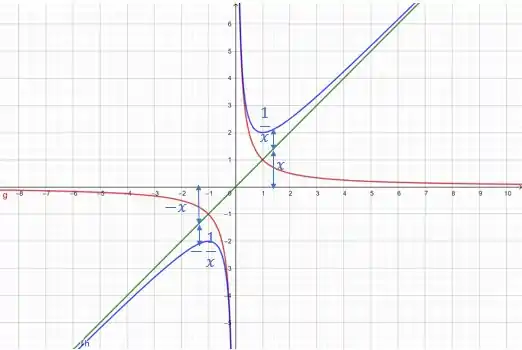
Então, repare que, para um mesmo , pegamos os valores das funções (no mesmo ponto) e e somamos! Fazendo isso para todos os pontos dos gráficos, chegamos na curva em azul, que é !

Agora, só o gráfico que nos interessa:

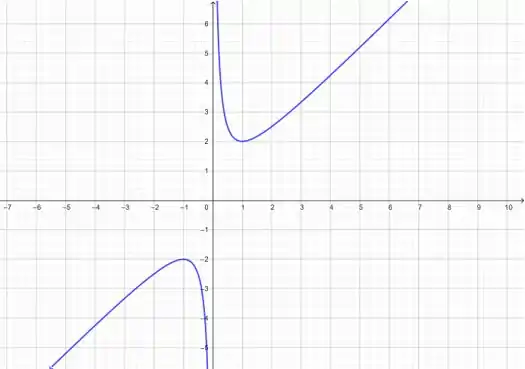
Esse é o gráfico de .

Obs.: já usamos o recurso gráfico para mostrar a resposta para você 😊então, vamos encerrar por aqui!!