Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.3 - Ex. 72
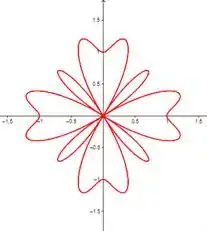
Use uma ferramenta gráfica para traçar a curva polar. Escolha o intervalo do parâmetro para ter certeza de que você fez a curva inteira.
Passo 1
Uma forma de analisar a curva formada, é através de procedimentos matemáticos. Podemos substituir ângulos e verificar o valor de .
Observe como varia à medida que aumenta de a ° (ou a ) no primeiro semicírculo da curva.
- Para e , . Isso indica que a curva começa e termina em no eixo horizontal (eixo ).
- Para , , sugere a curva atinge seu ponto mais distante do eixo polar (eixo ) no sentido positivo.
- Para e , . Ou seja, a curva passa pelo eixo polar (eixo ) e se estende para o lado oposto.
Passo 2
Com base nos valores de calculados, a curva parece ter uma forma complexa que se estende e se contrai ao longo do intervalo de . Além de ter vários pontos de máximo e mínimo, e outras características dependendo dos valores de considerados.
Sendo assim, podemos encontrar características da curva, no entanto, é complicado desenharmos sem o auxílio de um software gráfico.
Passo 3
Para esboçar essa curva, basta jogar a fórmula em uma ferramenta gráfica. Usarei aqui o site https://www.geogebra.org/m/F7avt32x mas você pode usar o de sua preferência.
Neste site, a única diferença é que usaremos o parâmetro no lugar de , mas isso não muda o resultado, basta considerar .
Para saber se o intervalo está traçando toda a curva, basta testar com um intervalo de a múltiplos de .
Passo 4
Para esta equação, o gráfico foi construído com o intervalo .
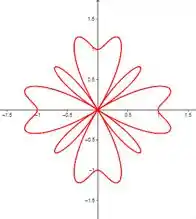
Resposta
