Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.4 - Ex. 3
Use o gráfico dado de para encontrar um número tal que
se então
Passo 1
E aí, galerinha, tudo joia? Não precisa assustar com essa questão, vem comigo resolver passo a passo!
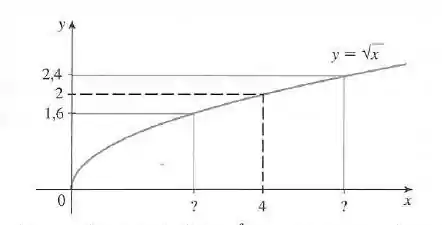
A ideia aqui é usar o gráfico abaixo da função para encontrar o número de modo que, se a diferença entre e for menor que , então a diferença entre e seja menor que .
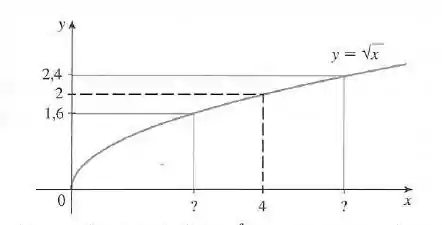
Então podemos usar a região próxima do ponto . Podemos reescrever a desigualdade
Com o objetivo de tirar o módulo e isolar o , teremos:
Assim, precisamos determinar os valores de para os quais a curva está entre as restas horizontais e .
Passo 2
Agora, olhando no gráfico as três funções próximo do ponto , e vemos o ponto de intersecção da curva com as retas não está no gráfico, entretando é possível achar apenas substituindo na curva :
Vemos que esse intervalo não é simétrico em torno de , a distância até a extremidade esquerda é , e a distância até a extremidade direita é .
Podemos escolher como o menor desses números, isto é . Embora tenhamos escolhido , qualquer valor menor positivo de também funcionaria.
E prontinho, finalizamos! Curtiu?