Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 4.3 - Ex. 1
Use o gráfico dado de para encontrar o seguinte:
- O maior intervalo aberto no qual é crescente
- O maior intervalo aberto no qual é decrescente
- O maior intervalo aberto no qual é côncava para cima
- O maior intervalo aberto no qual é côncava para baixo
- As coordenadas do ponto de inflexão.
Passo 1
Oieee personas, bora resolver mais uma questão?
O gráfico dado pelo enunciado é o seguinte:
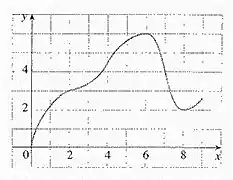
Então bora resolver essa belezinha?
Função Crescente e Decrescente:
- Crescente: A função sobe conforme nos movemos da esquerda para a direita no gráfico.
- Decrescente: A função desce conforme nos movemos da esquerda para a direita no gráfico.
Concavidade:
- Concavidade para Cima (Convexa): A curva se abre para cima, indicando que a taxa de crescimento da função está aumentando.
- Concavidade para Baixo (Côncava): A curva se abre para baixo, indicando que a taxa de crescimento da função está diminuindo.
Ponto de Inflexão:
- O ponto onde a concavidade da função muda de côncava para convexa, ou vice-versa, indica uma mudança na forma da curva.
Função Crescente:
Uma função é crescente em um intervalo se, para quaisquer e em com
Função Decrescente:
Uma função é decrescente em um intervalo se, para quaisquer em com .
Passo 2
Agora iremos determinar dos Intervalos Crescentes e Decrescentes
Intervalo Crescente:
- Observando o gráfico, é crescente entre e novamente entre
- Portanto, os maiores intervalos abertos onde é crescente são
Intervalo Decrescente:
- Observando o gráfico, são decrescentes entre
- Portanto, o maior intervalo aberto onde são decrescentes é .
Passo 3
Para a concavidade de uma Função, temos:
Concavidade para Cima (Convexa):
Uma função é côncava para cima em um intervalo se sua derivada segunda é positiva para todo em .
Concavidade para Baixo (Côncava):
Uma função é côncava para baixo em um intervalo se sua derivada segunda é negativa para todo em
Determinação dos Intervalos de Concavidade
Concavidade para Cima:
- Observando o gráfico, é côncava para cima entre e novamente entre .
- Portanto, os maiores intervalos abertos onde é côncava para cima são
Concavidade para Baixo:
- Observando o gráfico, é côncava para baixo entre e novamente entre
- Portanto, os maiores intervalos abertos onde é côncava para baixo são
Passo 4
Ponto de Inflexão
Ponto de Inflexão:
Um ponto de inflexão ocorre onde a função muda sua concavidade, de côncava para cima para côncava para baixo, ou vice-versa. Matematicamente, ocorre onde a derivada segunda muda de sinal.
Determinação dos Pontos de Inflexão
- Observando o gráfico, a concavidade de muda em
- Estimando os valores de no gráfico, as coordenadas dos pontos de inflexão são aproximadamente
Resposta
Maior intervalo crescente:
Maior intervalo decrescente:
Maior intervalo côncavo para cima:
Maior intervalo côncavo para baixo:
Coordenadas dos pontos de inflexão: